Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 05. 2011 11:05 — Editoval hradecek (26. 05. 2011 11:06)
Rovnica Kružnice - body, polomer
Ahoj, mám tu takýto príklad:
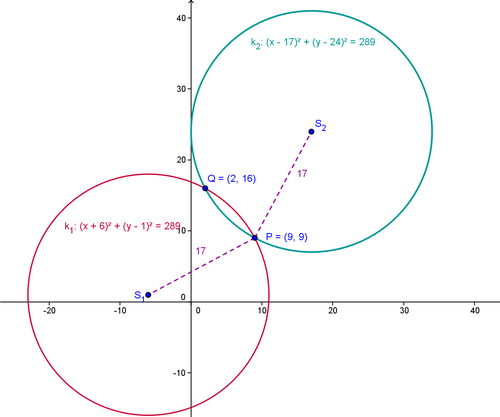
Kružnica prechádza bodmi ![kopírovat do textarea $P[9;9]$](/mathtex/b0/b0a7ae2742a64f94b6267f5cf8236e75.gif) ,
, ![kopírovat do textarea $Q[2;16]$](/mathtex/e2/e27eced3862a8dce8214782c575a1368.gif) a má daný polomer
a má daný polomer  . Napíšte jej stredový tvar
. Napíšte jej stredový tvar
Mňa napadlo, iba dosadiť si body a vyriešiť sústavu:
Z čoho mi vyšiel jeden veľký výraz: 
a z toho mi wolframalpha.comvypočítal 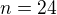 čo by podľa výsledkov aj sedelo...
čo by podľa výsledkov aj sedelo...
Ešte ma napadlo, že: 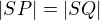 ale to by viedlo asi k tomu istému ;-)
ale to by viedlo asi k tomu istému ;-)
Ale ešte mi chýba jedno riešenie. Nejaké nápady ? najlepšie bez toho dlhého výraz ;-)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
- (téma jako vyřešené označil(a) hradecek)
#2 26. 05. 2011 11:48
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Rovnica Kružnice - body, polomer
↑ hradecek:
Tyto dvě rovnice:
si roznásob a uprav. Potom druhou rovnici odečti od té první, měl by vyjít výraz po úpravě 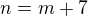 , což když dosadíš do jedné z původních rovnic, ti hodí kvadratickou rovnici o jedné neznámé
, což když dosadíš do jedné z původních rovnic, ti hodí kvadratickou rovnici o jedné neznámé
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 26. 05. 2011 11:58 — Editoval hradecek (26. 05. 2011 11:59)
Re: Rovnica Kružnice - body, polomer
Aha, no jasne dík.
Myslel som, že cez tak to bude oveľa ťažšie :)
a nemalo by to byť skôr 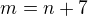 ? tak to vyšlo mne...
? tak to vyšlo mne...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#4 26. 05. 2011 13:12 — Editoval Cheop (26. 05. 2011 13:27)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Rovnica Kružnice - body, polomer
↑ hradecek:
Pravdu má kolegyňka ↑ Aquabellla:
Nikdo není dokonalý
Offline
#5 27. 05. 2011 13:12 — Editoval hradecek (27. 05. 2011 13:12)
Re: Rovnica Kružnice - body, polomer
↑ Aquabellla:
↑ Cheop:
Veľmi pekne ďakujem ;-)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline