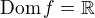Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2008 20:56
Log(stále >0)
Ahoj,
narazil jsem na příklad f(x)=Log(x^2 - 2x + 2) a měl bych určit definiční obor. Je jasné, že je tam podmínka ta ( ) >0 no aa a? dosazuju jak dosazuju je to stále >0. Ta závorka se týká samozrejme paraboly. Takže by měla být celá nad osou x, ale co to znamená pro ten logaritmus??? Že tam mohu dosadit jakékoliv číslo? A definiční obor je tedy R?
Díky
Offline
#4 30. 05. 2008 17:12
- halogan
- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Log(stále >0)
Závorka se týká kvadratické rovnice. Spočítáme diskriminant. 4 - 8 = -4. Diskriminant je záporný, takže rovnice nemá žádný průsečík s osou x a když je 
(před x^2) kladné, tak je _nad_ osou x a tím pádem je Df = R.
Offline