Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » statistika a pravdepodobnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 05. 2008 23:10
statistika a pravdepodobnost
vedel by mi niekto poradit s tymito prikladami.potreboval by som to vysvetlit aby som to pochopil ak sa da. vopred dakujem...
1. Na morskom pobreží práve dovolenkuje žien, mužov a detí. Medzi ženami je neplavcov, medzi mužmi plavcov a medzi de?mi plavcov. Plávacie koleso si práve zakúpil jeden dovolenkár. Aká je pravdepodobnos?, že je to neplavec?
2. Určte asymetriu Alfa(X) základného súboru: 2,8 3,5 1,9 2,4 3,1 a výsledok porovnajte s tzv. excelovskou asymetriou.
3. Pravdepodobnos? zakúpenia zahraničného zájazdu v spoločnosti Tour jedným klientom je 0,25. V pobočkách cestovnej kancelárii je práve 250 záujemcov, určte pravdepodobnos? toho, že zahraničný zájazd si zakúpi nie menej ako 200 záujemcov. Aplikujte asymptotické vzorce.
Offline
#2 31. 05. 2008 00:31
Re: statistika a pravdepodobnost
Precti si po sobe, zda tvuj prispevek opravdu vypada, tak jak ma :) v prvnim priklade nejsou cisla, efektivne si tak zamezujes moznost odpovedi ;-)
Lasciate ogni speranza. | Podílí se na Encyklopedii Fyziky (http://fyzika.jreichl.com) | Oblíbený IT projekt http://online-domain-tools.com
Offline
#3 31. 05. 2008 15:26
Re: statistika a pravdepodobnost
Může mně někdo poradit jaký zápis bude na pravé straně rovnice, P(y) když:
( P(w) > 15 ) = 1 - P(w) < 15 slovně P(w) je větší jak 15 = 1 - P(w) je je menší nebo se rovna 15
=
P(y) > 4 = ? a P(y) > 5 = ? znak = na řádku pod znake > a <
= =
Offline
#4 31. 05. 2008 22:19 — Editoval jelena (31. 05. 2008 22:19)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: statistika a pravdepodobnost
↑ miroslav:
pokud jsem dobre lustila, tak tento zapis znamena:
( P(w) > 15 ) = 1 - (P(w) <= 15) doplnila jsem zavorky
"pravdepodobnost jevu, ze "neceho bude vic nez 15" se rovna (1 - "pravdepodobnost jevu opacneho") (ze neceho bude mene nebo se rovno 15)
(P(y) >= 4) = 1 - (P(y) < 4) ">=" "vetsi nebo se rovna" se meni na "< mensi"
(P(y) >= 5) = 1- ((P(y) < 5)
Staci to tak?
Offline
#6 03. 06. 2008 19:50
Re: statistika a pravdepodobnost
Zdravim
doufam, ze by mi nekdo mohl poradit.
Mam Poisson distribution s parametrem μ = 2.2
Mam take zadano c.d.f.
x 0 1 2 3 4 5 6 ....
F(x) 0.1108 0.3546 0.6227 0.8193 0.9275 0.9751 0.9925
Jak vypocitam lower quartile - ql or upper quartile - qu ?
Predem dekuji
Offline
#8 04. 06. 2008 11:23
Re: statistika a pravdepodobnost
1. Na morskom pobreží práve dovolenkuje 35% žien, 40% mužov a 20% detí. Medzi ženami je 30% neplavcov, medzi mužmi 25%plavcov a medzi de?mi 50% plavcov. Plávacie koleso si práve zakúpil jeden dovolenkár. Aká je pravdepodobnos?, že je to neplavec?
Offline
#9 04. 06. 2008 13:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: statistika a pravdepodobnost
↑ kein.007:
Zvlastni uloha :-) do 100 % neco chybi (mame zeny, muze, deti v souctu 95 %, kdo jsou zbyvajici 5 % - hm :-)
Nicmene, to asi bude tak (zkusim to dkonce pojmenovat - "podminena pravdepodobnost", Bayesuv vzorec)
35% žien, 30% neplavcov
40% mužov, z toho 25%plavcov, tedy neplavcu 75 %
20% detí, z toho 50% plavcov, tedy neplavcu 50 %
Pravdepodobnost, ze kolo zakoupil neplavec - jev A za podminky, ze byl z urcite skupiny:
P(A) = P(A/B1)*P(B1) + P(A/B2) * P(B2)+ P(A/B3)*P(B3) = 0,3 *0,35 + 0,75 *0,4 + 0,5 *0,2
OK?
Offline
#10 05. 06. 2008 13:29
Re: statistika a pravdepodobnost
vie mi niekto poradi? s príkladom: určte pravdepod. toho, že jav A nastane práve osemdesiatkrát v 400 nezávislých pokusoch, ak pravdepodobnos? výskytu javu A je v každom pokuse rovné 0,2. použite asymptotické vzorce. Ďakujem
Offline
#11 05. 06. 2008 13:31
Re: statistika a pravdepodobnost
Ahojte.
prosím ešte o jeden príklad. v ponuke CK sa objaila nová destinácia Vian.ostrovy. pravdepodobnos? zakúpenia tejto destinácie jedným klientom je 2/3. v CK sa nachádzajú štyria klienti. vypočítajte najpravdepodobnejšiu hodnotu Ko a P4Ko. Ďakujem
Offline
#12 07. 06. 2008 13:34
Re: statistika a pravdepodobnost
Dekuji moc Plisni za pomoc s mym predchozim prikladem. Mam jeste jeden se kterym si nevim rady.
Nezavisle vzorky byly brany ze dvou normalne distribuovane populace s stejnou varianci. Vzorek 1, z populace 1, obsahuje 7 a ma vzorkovou variaci 5.104. Vzorek 2, z populace 2, obsahuje 10 a ma vzorkovou variaci 6.65.
Jak odhadnu celkovou spolecnou standardni odchylku a jak vypocitam t-quantile pro 95% interval spolehlivosti?
predem dekuji
Offline
#13 08. 06. 2008 18:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: statistika a pravdepodobnost
↑ kein.007:
Jelikoz mam za ukol se zlepsovat ve statistice a pravdepodobnosti, tak zde jsou moje pokusy:
2. Určte asymetriu Alfa(X) základného súboru: 2,8 3,5 1,9 2,4 3,1 a výsledok porovnajte s tzv. excelovskou asymetriou
Muj navrh:
- excelovskou asymetrii zjistime pomoci nastroje Analyza dat - popisna statistika, koeficient sikmosti (to bylo rychle a vyslo mi to -0,257
- rucni zpracovani (vzorce) - pres prumer a smerodatnou odchylku - sestavime tabulku hodnot x1, x2, x3 x4, x5, najdeme prumer a pouzijeme upraveny vzorec pro koeficient sikmosti: - vzorce jsou kopirovany z wikipedie
- vzorce jsou kopirovany z wikipedie
U prikladu 2 - nevaham a doufam, ze dobre, ale tady vaham:
3. Pravdepodobnos? zakúpenia zahraničného zájazdu v spoločnosti Tour jedným klientom je 0,25. V pobočkách cestovnej kancelárii je práve 250 záujemcov, určte pravdepodobnos? toho, že zahraničný zájazd si zakúpi nie menej ako 200 záujemcov. Aplikujte asymptotické vzorce.
Opet navrh - Binomicke rozdeleni s n = 250, p = 0,25. Kontroluji podminky, cim mohu aproximovat - pro aproximaci Poissonem neni splnena podminka (dostatecne male p), pro aproximaci normalnim n*p(1-p)=250*0,25*(1-0,25)=46,9 je to vetsi, nez 9 - aproximuji normalnim rozdelenim s 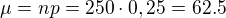 a
a 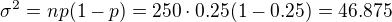
A tady zacinam vahat:-) , ted premyslim, jak se to hleda v tabulkach a zda neni chyba, ze jsem nepouzila normovanou hodnotu a zda to vubec dobre :-(
, ted premyslim, jak se to hleda v tabulkach a zda neni chyba, ze jsem nepouzila normovanou hodnotu a zda to vubec dobre :-(
Tak kdybyste se nekdo podival, budu vdecna :-)
Offline
#14 08. 06. 2008 18:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: statistika a pravdepodobnost
↑ viktoria:
V ponuke CK sa objaila nová destinácia Vian.ostrovy. Pravdepodobnos? zakúpenia tejto destinácie jedným klientom je 2/3. v CK sa nachádzajú štyria klienti. Vypočítajte najpravdepodobnejšiu hodnotu Ko a P4 Ko.
Opet pouze navrh :-)
Schema Bernoulliho
mame n=4, p=2/3 (zakoupeni), q=1-p=1/3 (nezakoupeni). Nekpravdepodobnejsi hodnota k se ma nachazet v intervalu od (np-q) do (np+p), tedy od 7/3 do 10/3 a ma to byt hodnota celociselna. V tomto intevaru se nachazi Ko = 3.
P4 (3) = C(4 nad 3) * (2/3)^3 * (1/3)^1 = 32/81 asi 0,395.
1. priklad od ↑ viktoria: je na stejnem principu jako to, co jsem se pokousela resit v predchoyim prispevku.
Dekuji za kontrolu :-)
Offline
#15 08. 06. 2008 19:50
Re: statistika a pravdepodobnost
↑ jelena:
Priklad 3: Takovou uvahu ospravedlnuje takzvana centralni limitni veta, cili princip reseni je podle meho dobre. Scitame 250 velicin z alternativniho rozdeleni, tento soucet ma potom priblizne rozdeleni normalni.
↑ jelena:
Tady nemuzu moc posoudit co je dobre a co ne, nebot nerozumim symbolum Ko a P4 Ko.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#17 15. 06. 2008 23:22
Re: statistika a pravdepodobnost
1. Na každom z troch úsekov A1, A2, A3 diaľnice v smere Prešov – Bratislava sú vykonávané dopravné kontroly. Pravdepodobnos? kontroly motorového vozidla je pre jednotlivé úseky rovná:P(A1)=0,7 P(A2)=0,8 P(A3) =0,9 . Aká je pravdepodobnos?, že motorové vozidlo bude kontrolované aspoň na dvoch úsekoch diaľnice
2. Na univerzite je 1000 počítačov pripojených k sieti Internet a na obrazovke 200 počítačov priemerne je natiahnutá univerzitná webová stránka. Pomocou asymptotických vzorcov určte pravdepodobnos?, že uvedená stránka je na obrazovkách 200 až 300 počítačov univerzity
3. Číslo x vyberieme z intervalu[1,3] , číslo y vyberieme z intervalu [2,4] . Aká je pravdepodobnos?, že dvojnásobok čísla y mínus jedennásobok čísla x je väčší ako tri?
4. Vo vestibule hotela je pripravený vý?ah, ktorý tri osoby A, B, C vyvezie na 1. alebo 2. poschodie. Aká je pravdepodobnos?, že aspoň jedna osoba vystúpi na 1. poschodí?
5. V cestovnej kancelárii sú dvaja klienti. Prvý klient si zakúpi fakultatívny výlet s pravdepodobnos?ou p 1 = 0,7 a druhý klient s pravdepodobnos?ou p2 = 0,4. Určte rozdelenie pravdepodobnosti zakúpenia fakultatívneho výletu dvomi klientmi
6. Počítač náhodne generuje čísla x patri (2,4) y patri (3,6). Počítač vyhráva, ak y je mensie ako 2x-2 , hráč v opačnom prípade. Určte pravdepodobnos? pre výhru hráča
7. CK ponúka domáce zájazdy v cene 1, 3, 5, 7 p. j. a zahraničné zájazdy v cene 10, 20, 40, 60, 80 p. j. Klient sa rozhodol zakúpi? jeden domáci a jeden zahraničný zájazd. Aká je pravdepodobnos?, že bude zakúpená dvojica zájazdov v cene najmenej 64 p. j., ak viete, že bol zakúpený zájazd v cene 60 p. j.
Offline
#18 16. 06. 2008 01:12 — Editoval ttopi (16. 06. 2008 01:18)
Re: statistika a pravdepodobnost
3. Z obrázku mi plyne P=75%
Zakreslím do kartézské soustavy oba intervaly, určím funkci pro závislost y na x a načrtnu křivku. Tou je přímka, která mi to dělí na 75% tak, aby byla podmínka splněna.
6.Podobný případ. Funkce mi dělí graf na 5/8 pro hráče a 3/8 pro PC. Takže P hráče by měla být 62,5%.
oo^0 = 1
Offline
#21 18. 06. 2008 22:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: statistika a pravdepodobnost
↑ ttopi:
Rozumis tomu, co ten nas kolega podnika s prispevky?
Pristupoval jsi k tomu jako permutace s opakovanim?
A nemas hledet do geometrie? - vychovna poznamka :-)
Offline
#23 19. 06. 2008 00:00
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: statistika a pravdepodobnost
↑ VladaPi:
Kolega ttopi to uz vyresil :
V pripade, ze by dcera potrebovala pres vzorce na kombinace, variace, permutace, tak ta moznost je takova:
Slovo NOROVO se sklada celkem ze 6 prvku, z toho 3 prvky se opakuji, ostati jsou po 1. Vsech moznych anagram sestavime tak, ze budeme premistovat pismenka - to znamena permutace. jelikoz nektery z prvku se opakuje - pak permutace s opakovanim
Pravdepodobnost jevu A - "na prvni pozici je pismeno O" :
pocet vsech slov s pocatkem O
P(A) =-------------------
pocet vsech moznych slov
Vzorec pro permutaci s opakovanim vypada takto: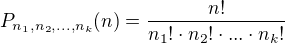 ,
,
v nasem pripade - pocet vsech moznych slov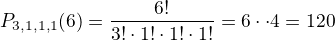 ,
,
pocet vsech slov s pocatecnim pismenem O (prakticky to provedeme tak, ze jedno O pevne umistime na zacatek a permutaci budeme tvorit ze zbyvajicich 5 pismen 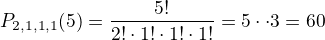 ,
,
Pravdepodobnost P(A)= 60/120 = 0,5, coz je stejny vysledek jak u kolegy ttopi
tady jsou vzorce, co mozna budete potrebovat (dcera by to mela mit i v ucebnici):
http://cs.wikipedia.org/wiki/Permutace# … A1n.C3.ADm
http://cs.wikipedia.org/wiki/Variace_%2 … atorika%29
http://cs.wikipedia.org/wiki/Kombinace
http://cs.wikipedia.org/wiki/Pravd%C4%9Bpodobnost
Offline
#24 19. 06. 2008 06:19
Re: statistika a pravdepodobnost
↑ jelena:
Moje řešení je podstatně jednodušší, protože jsem si úlohu značně zjednodušil. Mě v podstatě zajímá jen první písmenko, tak jsem to tak řešil. Na první pozici mám 6 možností, z toho 3 kladné, takže 1/2.
Jdu si ještě opakovat, ale moc toho neumím. Jsem tam sám, ostatní se asi strachy odepsali :-(
oo^0 = 1
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » statistika a pravdepodobnost (TOTO TÉMA JE VYŘEŠENÉ)

 . v pripade dolniho kvartilu je p = 0,25 a pro horni kvartil je p = 0,75. takze v nasem pripade mame
. v pripade dolniho kvartilu je p = 0,25 a pro horni kvartil je p = 0,75. takze v nasem pripade mame  .
.