Matematické Fórum

pololilo · 02. 06. 2011 13:44

Zdravím, tenhle příklad jsem našel v ukázkových testech.
Můžete mi poradit, jak mám postupovat?
Děkuju předem

Phate · 02. 06. 2011 13:49

Dokazes zapsat k-ty prvek toho rozvoje?

pololilo · 02. 06. 2011 14:00

↑ Phate:

asi ne :(

Phate · 02. 06. 2011 14:03

↑ pololilo:
vis, jak vypada binomicky rozvoj?

pololilo · 02. 06. 2011 14:05

↑ Phate:

Já právě vůbec nevim. Tohle jsme ve škole nebrali.

jarrro · 02. 06. 2011 14:06

použi binomickú vetu

Cheop · 02. 06. 2011 14:06

↑ pololilo:
Zkus se podívat Tady

pololilo · 02. 06. 2011 14:25

↑ Cheop:

hm, tak tohle nepohlo

↑ jarrro:

jarrro já to v těch vzorcích nevidím, nemohl bys mi napsat postup? já potom pochopim co po mě chtějí.

jarrro · 02. 06. 2011 14:30

↑ pololilo:rozpíš tú mocninu pomocou binomickej vety a uvidíš to

pololilo · 02. 06. 2011 14:35

↑ jarrro:

Jak můžu podle tohodle něco rozepsat :-)

standyk

↑ pololilo:

$\left(\sqrt[3]{x}-\frac{2}{x}\right)^{10}$

Tvar binomického rozvoja vidíš v odkaze ktorý ti poslal napr. ↑ Cheop::
${n \choose k} \cdot {\left(\sqrt[3]{x}\right)}^{n-k}\cdot {\left(-\frac{2}{x}\right)}^{k} = x^{-6}$
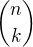${10 \choose k} \cdot {\left(\sqrt[3]{x}\right)}^{10-k}\cdot {\left(-\frac{2}{x}\right)}^{k} = x^{-6}$ Tu môžeš ignorovať absolútne členy: namiesto $-\frac{2}{x}$ môžeš počítať s $\frac{1}{x}$ a ${n \choose k}$ môžeš v tomto kroku ignorovať taktiež.
Dostávaš tak zjednodušený vzorec ktorým vypočítaš k.-ty člen:
${\left(\sqrt[3]{x}\right)}^{10-k}\cdot {\left(\frac{1}{x}\right)}^{k} = x^{-6}$

Pokračuj a vypočítaj čomu sa rovná k - čiže ktorý člen binomickéh rozvoja má člen 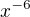$x^{-6}$ Potom dosaď do tohto vzorca:
${n \choose k} \cdot {\left(\sqrt[3]{x}\right)}^{n-k}\cdot {\left(-\frac{2}{x}\right)}^{k} = x^{-6}$

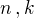$n\,, k$ už budeš poznať. Potom už jednoducho dopočítaš konkrétny koeficient pri k.-tom člene...

pololilo · 02. 06. 2011 14:50

↑ standyk:

díky ti moc standyk, problém je v tom, že já nevim, jak se taková rovnice řeší.

standyk

↑ pololilo:

Toto musíš vedieť vypočítať, sú to len jednoduché mocniny:
${\left(\sqrt[3]{x}\right)}^{10-k}\cdot {\left(\frac{1}{x}\right)}^{k} = x^{-6}$
${\left(x^{\frac{1}{3}}\right)}^{10-k}\cdot {\left(x^{-1}\right)}^{k} = x^{-6}$
$x^{\left(\frac{10}{3}-\frac{k}{3}\right)} \cdot {x^{-k}} = x^{-6}$
$\ldots$

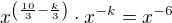
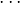
Takto pokračuj ... x môžeš zanedbať a počítaj len s mocninami. vypočítaš $k=\ldots$
Týmto vypočítaš ktorý člen binomického rozvoja obsahuje 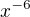$x^{-6}$
Ďalej pokračuj ako som ti písal vyššie. Dosaď do vzorca binomického rozvoja

EDIT: Ak nechápeš binomickému rozvoju tak ten si musíš rozhodne naštudovať lebo tu sa bez neho nepohneš. Ako Cheop písal tu máš celkom dobrý: odkaz
Zhodou náhod je celý príklad prezentovaný aj tu :)

pololilo · 02. 06. 2011 15:04

↑ standyk:

pro k mi tam vyšla kvadratická rovnice

pololilo · 02. 06. 2011 15:05

↑ standyk:

ok kouknu na ten odkaz, díky

standyk · 02. 06. 2011 15:09

↑ pololilo:

Žiadna kvadratická rovnica nevznikne. Exponenty nenásobíš ale sčítaváš. Použi vzorec: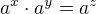

$a^x\cdot a^y = a^z$ a teda: $x\color{red}+\color{black}y=z$

pololilo · 02. 06. 2011 15:23

↑ standyk:

jak by to vypadalo v tomhle příkladě?

Tam je 2x

výsledek má být B: je nutný si to takhle rozepisovat?

standyk

↑ pololilo:

Daj to ale najprv do novej témy lebo si to tu už nikto nevšimne...

EDIT:
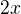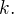Riešiť to budeš presne tak isto ako ten predtým. To $2x$ nič nemení na veci. Prepíšeš si to na $(2x)^{\frac12}$ a riešiš rovnako... Najprv $k.$ -ty člen a potom odtiaľ výsledný koeficient...

Rumburak · 02. 06. 2011 16:59

↑ standyk:

Ahoj, je mi jasné, že umíš úlohu vyřešit a máš poctivou snahu poradit kolegovi, ale rovnice

${n \choose k} \cdot {\left(\sqrt[3]{x}\right)}^{n-k}\cdot {\left(-\frac{2}{x}\right)}^{k} = x^{-6}$ resp. ${10 \choose k} \cdot {\left(\sqrt[3]{x}\right)}^{10-k}\cdot {\left(-\frac{2}{x}\right)}^{k} = x^{-6}$

jsou bohužel nesprávné, protože na jejích pravé straně chybí činitel

${n \choose k}(-2)^k$ resp. ${10 \choose k}(-2)^k$ .

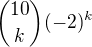Ten sice na řešení úlohy nemá vliv, nicméně matematická rovnice by měla být zapsána správně, zde například ve tvaru

${n \choose k} \cdot {\left(\sqrt[3]{x}\right)}^{n-k}\cdot {\left(-\frac{2}{x}\right)}^{k} = A_{n,k}\,x^{-6}$ ,

třeba s poznámkou, že $A_{n,k}$ je číslo, které je nezávislé na x a jehož bližší hodnota či vyjádření nás (momentálně) nezajímá.
Nepřesný výklad může být matoucí, je-li podán někomu, kdo s matematikou evidentně zápolí a sám si "korekci s konstantou $A_{n,k}$ "
neumí domyslet.

standyk · 02. 06. 2011 17:17

↑ Rumburak:

Áno, to je pravda. Dúfam že som tým zbytočne nepomýlil tázateľa. Ďakujem za pripomienku.. :)

petulinka332 · 30. 05. 2013 17:10

Ahoj!! Mam podobny priklad: urcit koeficient x2 v binomickem rozvoji (treti odmocnina z x + 2/x) na 10 ... x se nerovna nula... Ke clenu jsem se dostala ale nemohu se dopocitat ke koeficientu potom co dosadim k, spravny vysledek by mel byt ( 10 4) * 2 na ctvrtou, poradite mi jak se k tomu dostanu? Dekuji!!

bejf · 30. 05. 2013 18:12 — Editoval bejf (30. 05. 2013 18:17)

↑ petulinka332:
Zaprvé by bylo více než vhodné si založit vlastní téma. Za druhé by bylo vhodné příklad napsat v LaTeXu pro přehlednost (máš k dispozici při psaní příspěvku vpravo).
A za třetí, tedy vyjímečně ke Tvému příkladu:

Píšeš, že máš určit koeficient u $x^2$ zřejmě v binomickém rozvoji $$\sqrt[3]{x}+\frac{2}{x}$$ .

To zjistíš při rozepsání binomického rozvoje.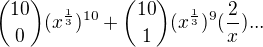
${10 \choose 0}(x^{\frac{1}{3}})^{10}+{10 \choose 1}(x^{\frac{1}{3}})^9(\frac{2}{x})...$

Tady se zastavím, protože mám podezření, že by v druhém členu mohlo vzniknout nějak $x^2$ .
${10 \choose 1}(x^{\frac{1}{3}})^9(\frac{2}{x}={10 \choose 1}\cdot x^3\cdot \frac{2}{x}$
xka se mi zkrátí a mám 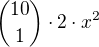${10 \choose 1}\cdot 2\cdot x^{2}$ .
Takže by měl být koeficient ${10 \choose 1}\cdot 2$ .

Jenže ty uvádíš výsledek 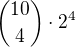${10 \choose 4}\cdot 2^4$ , což platí pro pátý člen.

Zkusme si to rozebrat. Pátý člen daného binomického rozvoje dostaneme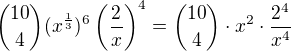
${10 \choose 4 }(x^{\frac{1}{3}})^6$\frac{2}{x}$^4={10 \choose 4}\cdot x^2 \cdot \frac{2^4}{x^4}$
xka se opět zkrátí a v tom zlomku ve jmenovateli bude $x^2$ sice, což je ovšem ${10 \choose 4}2^4\cdot x^{-2}$ .

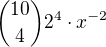Takže buď máš ty blbě zadání nebo oni blbě výsledek.

petulinka332 · 31. 05. 2013 12:21

Ahoj, omlouvam se, za to ze jsem se k nekomu vecpala do tematu a ze jsem to nenapsala spravne, jak to ma byt. Bohuzel jsem na teto strance od vcera nova a neorientovala jsem se tady, byla jsem rada, ze jsem aspon napsala svuj problem.

Diky moc za velkou pomoc!

Protoze jsem si nevedela rady s tim, jestli to mam vypocitane spravne ci ne, vyslo mi k 1 a po dosazeni mi vyslo to same co tobe ( 10 1) * 2, takze ted uz vim diky tobe, ze to maji oni jako spatnou spravnou odpoved a nebo blbe zadani, je to test z onlinu na strankach VSE.

Tak jeste jednou diky!!!!

Cheop · 31. 05. 2013 12:26

↑ bejf:
Zdravím ,
ten výsledek by byl dobře pokud by otázka zněla:
"Jaký koeficient bude u členu" s $x^{-2}$ no a osobně si myslím, že při přepisu se přehlédlo to mínus.

Matematické Fórum

#1 02. 06. 2011 13:44

Koeficient v binomickém rozvoji (přijímačky VŠE)

#2 02. 06. 2011 13:49

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#3 02. 06. 2011 14:00

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#4 02. 06. 2011 14:03

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#5 02. 06. 2011 14:05

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#6 02. 06. 2011 14:06

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#7 02. 06. 2011 14:06

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#8 02. 06. 2011 14:25

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#9 02. 06. 2011 14:30

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#10 02. 06. 2011 14:35

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#11 02. 06. 2011 14:36 — Editoval standyk (02. 06. 2011 14:46)

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#12 02. 06. 2011 14:50

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#13 02. 06. 2011 14:57 — Editoval standyk (02. 06. 2011 15:21)

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#14 02. 06. 2011 15:04

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#15 02. 06. 2011 15:05

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#16 02. 06. 2011 15:09

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#17 02. 06. 2011 15:23

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#18 02. 06. 2011 15:25 — Editoval standyk (02. 06. 2011 15:32)

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#19 02. 06. 2011 16:59

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#20 02. 06. 2011 17:17

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#21 30. 05. 2013 17:10

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#22 30. 05. 2013 18:12 — Editoval bejf (30. 05. 2013 18:17)

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#23 31. 05. 2013 12:21

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

#24 31. 05. 2013 12:26

Re: Koeficient v binomickém rozvoji (přijímačky VŠE)

Zápatí