Matematické Fórum

vysoka · 05. 06. 2011 20:51 — Editoval vysoka (05. 06. 2011 20:53)

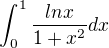$\int_0^1\frac{lnx} {1+x^2}dx$ ako zistujem takyto integral nejde normalnou metodou vyratat :( ked ho ratam ako neurcity... urcity je to plocha pod X http://www.wolframalpha.com/input/?i=in … rom+0+to+1 vopred vdaka ...zajtra mozno budem takyto potrebovat ....

Rumburak

Problém by mohlo činit pouze chování funkce ln x v blízkosti bodu 0, v němž má limitu zprava -oo . Pro 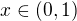$x \in (0, 1)$ je

$1 < 1 + x^2 < 2$ ,
$1> \frac {1}{1 + x^2} > \frac {1}{2}$ ,
(1) $\ln x < \frac {\ln x}{1 + x^2} < \frac {1}{2}\,\ln x\,\,\,\, (< 0)$ (protože $\ln x < 0$ ) .

Z odhadu (1) lze usoudit, že 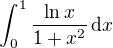$\int_0^1\frac{\ln x} {1+x^2}\,\mathrm{d}x$ konverguje tehdy a jen tehdy, konvergeje-li $\int_0^1 \ln x \,\mathrm{d}x$ .
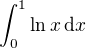Jak je to s konvergencí toho druhého integrálu ?

vysoka · 06. 06. 2011 13:03

↑ Rumburak: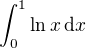 $\int_0^1 \ln x \,\mathrm{d}x$ konverguje kedze vysledok je -1
dakujem ... ale nanestastie sa takyto priklad nevyskytol ... vyskytla sa este zaujimavejsia vec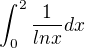
$\int_0^2 \frac{1}{lnx}dx$
http://www.wolframalpha.com/input/?i=in … rom+0+to+2 tu aspon povedalo ze nekonverguje ...aj ked ja som myslel ze konverguje .... :( tam som rozdelil integral na dva hranicou od 0-1 a 1-2 ale to mi aj tak nejak nepomohlo ....

Rumburak

Tady činí problém chování funkce v okolí bodu 1. Platí 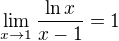$\lim_{x \to 1} \frac {\ln x}{x-1} = 1$ , takže co do existence či konvergence můžeme
místo integrálu

$\int_{1-\delta}^{1+\delta} \frac{1}{\ln x}\,\mathrm{d}x\,, \,\,\,\delta \in (0, 1)$

se stejným výsledkem zkoumat integrál

$\int_{1-\delta}^{1+\delta} \frac{1}{x-1}\,\mathrm{d}x\,, \,\,\,\delta \in (0, 1)$ .

Autor skryl část textu. Zobrazit/skrýt!

vysoka · 06. 06. 2011 22:43

↑ Rumburak:vdaka ...asi bude treba viac teorie sutdovat :)

Matematické Fórum

#1 05. 06. 2011 20:51 — Editoval vysoka (05. 06. 2011 20:53)

konvergencia integralu

#2 06. 06. 2011 10:24 — Editoval Rumburak (06. 06. 2011 10:27)

Re: konvergencia integralu

#3 06. 06. 2011 13:03

Re: konvergencia integralu

#4 06. 06. 2011 13:32 — Editoval Rumburak (07. 06. 2011 09:04)

Re: konvergencia integralu

#5 06. 06. 2011 22:43

Re: konvergencia integralu

Zápatí