Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 06. 2011 13:21
- check_drummer

- Příspěvky: 4899
- Reputace: 105
Re: inverse (ii)
↑ stuart clark:
Hi, by the way - where do you find inspiration for your problems - you think them up by yourself or do they come from some book or so? Thanks.
"Máte úhel beta." "No to nemám."
Offline
#3 17. 06. 2011 13:34 — Editoval Pavel (17. 06. 2011 13:34)
Re: inverse (ii)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 19. 06. 2011 19:35
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: inverse (ii)
Thanks check_drummer.
@check_drummer ,taken from book
Thanks Paul, I also have a solution , but very lengthy.
anyway can you show your solution.
Thanks to all.
Offline
#5 23. 06. 2011 10:34
Re: inverse (ii)
↑ stuart clark:
Before I show my solution, I would like to clarify the definition of 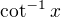 . There exist two concept, see Inverse cotangent and the paragraph There are at least two possible conventions for defining the inverse cotangent... Which of them is supposed in your problem? The one with the range
. There exist two concept, see Inverse cotangent and the paragraph There are at least two possible conventions for defining the inverse cotangent... Which of them is supposed in your problem? The one with the range 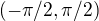 that is not continous at 0, or the one with the range
that is not continous at 0, or the one with the range  that is continous anywhere in
that is continous anywhere in 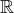 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
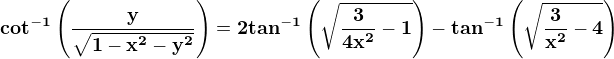
 and
and  .
.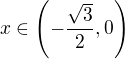 then
then 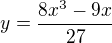 .
.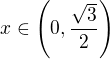 then
then 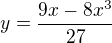 .
.