Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Anketa
"Mě by třeba zajímalo, jak jste se sem na forum vůbec dostali :-)"(c)
| Cíleně jsem hledal(a) nějaké Matematické fórum. | 30% - 82 | |||||
| Hledal(a) jsem pomoc s matematikou (jsem studující). | 37% - 101 | |||||
| Hledal(a) jsem pomoc s matematikou (jsem vyučující). | 1% - 4 | |||||
| Potřeboval(a) jsem řešení problému z praxe. | 3% - 8 | |||||
| Fórum mi bylo doporučeno. | 5% - 14 | |||||
| Jiná cesta, případně doplním v tématu "O nás :-)". | 4% - 13 | |||||
| V čtenářském deníku mi chybela kniha "Stařec a moře". | 1% - 5 | |||||
| Hledal(a) jsem zdroj řešení projektů svých studentů. | 0% - 2 | |||||
| Hledal(a) jsem kružítko. | 5% - 15 | |||||
| Už si nepamatuji. | 8% - 22 | |||||
| Počet hlasujících: 228 | ||||||
#126 08. 07. 2008 12:15
#128 08. 07. 2008 15:56
#129 08. 07. 2008 17:12 — Editoval Chrpa (08. 07. 2008 17:13)
Re: O nas :-)
Píšu jako Chrpa = Cheop
Malá nápověda:
Ta kachna bude plavat na soustředné kružnici tak, aby její relativní rychlost ve vodě byla stejná jako rychlost lišky na břehu
Teď už bys měl sestavit správně i druhou rovnici a vypočítat požadované rychlosti.
Offline
#130 08. 07. 2008 18:49
Re: O nas :-)
Aha, tak to mě nenapadlo. Já myslel, že nejefektivnější cesta je ta nejkratší, což je ta od středu ke kraji, čili 3 metry.
Zdá se tedy, že řešení může být i více, protože moje navrhované řešení zdá se odpovídá celkem výsledku.
oo^0 = 1
Offline
#131 09. 07. 2008 06:40
#132 09. 07. 2008 08:15 — Editoval Cheop (09. 07. 2008 10:30)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: O nas :-)
Ještě k úloze
"Líný vrabec"
Úloha se dá řešit i takto:
Dle obrázku musí platit: 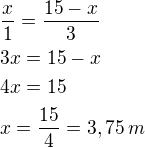
Vzdálenost, ve které musí vrabec sezobnout žížalu je 3,75 m od plotu.
Pokud vzdálenost x dosadíme do rovnice: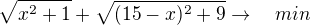 pak vrabec proletí vzdálenost:
pak vrabec proletí vzdálenost: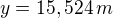
Nebo celková vzdálenost vrabce je: (dle obrázku)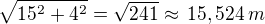
Nikdo není dokonalý
Offline
#133 09. 07. 2008 09:37 — Editoval Cheop (09. 07. 2008 09:50)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: O nas :-)
K požadavku paní Jeleny ohledně pěkných řešení.
U úlohy Líný vrabec by zadání mohlo být toto: (pak výsledek vyjde pěkné číslo)
Vrabec sedí na plotu vysokém 3 m. Ve vzdálenosti 12 m od plotu je strom, který má větev ve výšce 6 m.
Mezi plotem a stromem jsou hustě rozesety žížaly.
V jaké vzdálenosti od plotu musí vrabec sezobnout žížalu, aby proletěl trasu plot - žížala - větev po přímkách a po nejkratší dráze.
Jelenko můžeš počítat (všechna čísla by měla vyjít pěkně).
Nikdo není dokonalý
Offline
#134 09. 07. 2008 09:40
Re: O nas :-)
↑ Chrpa:
S těma soustřednýma kružnicema. Chápu to dobře tak, že kachna popluje na kružnici o 3x menším obvodu, aby se jejich rychlosti relativně vyrovnaly? Stejně pak ale musí udělat odbočku ke kraji ne?
Napiš mi už to řešení, říkám, nic víc nevymyslím, než jsem napsal :-)
oo^0 = 1
Offline
#135 09. 07. 2008 10:09 — Editoval Cheop (09. 07. 2008 11:54)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: O nas :-)
Dobře tady máš řešení:
Označme: v - rychlost lišky
v/3 - rychlost kachny (dle zadání)
t - čas lišky při honbě kachny
r - poloměr jezírka (3 m) - dle zadání
r1 - poloměr soustředné kružnice na ktaré plave kachna
x - vzdálenost, kterou musí kachna uplavat ke břehu
Pak musí platit: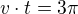 (1/2 obvodu jezírka - tuto vzdálenost musí uběhnout liška)
(1/2 obvodu jezírka - tuto vzdálenost musí uběhnout liška)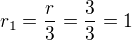 (soustředná kružnice bude mít poloměr 1 m) - relativní rychlost lišky a kachny je stejná
(soustředná kružnice bude mít poloměr 1 m) - relativní rychlost lišky a kachny je stejná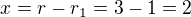 (tuto vzdálenost nusí uplavat kachna)
(tuto vzdálenost nusí uplavat kachna)
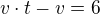
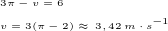 rychlost lišky
rychlost lišky rychlost kachny
rychlost kachny
Jak ttopi vídíš, tak kachna nepoplave ve vodě 3 m, ale pouze metry dva. Z hranice soustředné kružnice ke břehu.
Nikdo není dokonalý
Offline
#136 09. 07. 2008 10:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: O nas :-)
↑ Cheop:
Zdravim :-)
dekuji moc za odpoved a take za cisla - vedela jsem, koho o to pozadat, prece spravny ekonom musi umet vyrobit oku lahodici data :-)
Ja treba pracovne matematiku temer nepotrebuji, az na zpracovani vysledku - to mi staci EXCEL, vypocet procent a pocitani tak do 200 (i mene mozna) - s tim si vystacim docela dobre (ani vyplatu si nekontroluji, verim ekonomum :-) Psat ale musim moooc a ted opet budu (dopijim kavu a pujdu pokracovat ve psani :-)
↑ ttopi:
Take zdravim :-)
Pomucku to chce - tuzky s provazkem + spendliky :-) a kreslit :-)
Offline
#137 09. 07. 2008 12:04
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: O nas :-)
Aby "Fórum" přes prázdniny nezakrnělo mám tady trochu zamotaný příklad. (Když se rozmotá tak to není tak zlé).
Zadání:
Ivan a Emil
Ivanovi a Emilovi je dohromady 86 let. Počet let Ivana tvoří 15/16 stáří,
kterého dosáhne Emil, až věk Ivana bude 9/16 takového počtu let,
kterého by Emil dosáhl, kdyby se dožil takového stáří, které je 2x větší
než počet let Ivana v okamžiku, kdy bude Ivan 2x starší než Emil. Jak jsou staří?
Nikdo není dokonalý
Offline
#138 09. 07. 2008 14:42 — Editoval ttopi (09. 07. 2008 14:51)
Re: O nas :-)
Vychází celá čísla? Mě zatím nějak ne :-(
Napíšu postup, který jsem zvolil.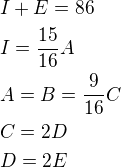
Kde jsem si písmeny A,B,C,D označil věky různých podmínek a rozepsal si, co podínka musí splňovat.
To jsem dal dohromady a vyšlo mi

což je samozřejmě špatně. A teď, kde je chyba :-)
EDIT:Sám tuším, že problém bude nejspíš v tom posledním E, protože E má být současný věk Emila a já použil E i pro věk, který je podmíněný určitými předchozími podmínkami.
oo^0 = 1
Offline
#139 09. 07. 2008 15:00 — Editoval Cheop (10. 07. 2008 10:58)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: O nas :-)
Kávomil
Délka části kruhu L je vlastně obvod podstavy kužele.
Musí tedy platit:
Z pravého obrázku platí: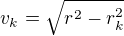
Objem kužele - má být maximální
- má být maximální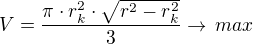 derivujeme dle
derivujeme dle 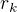 a dostaneme:
a dostaneme: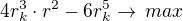 vydělíme
vydělíme 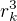 a dostaneme:
a dostaneme: dopočítáme
dopočítáme 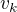
 dosadíme do rovnice (1) a dostaneme:
dosadíme do rovnice (1) a dostaneme: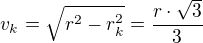
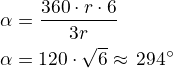
Nikdo není dokonalý
Offline
#142 09. 07. 2008 15:21 — Editoval ttopi (09. 07. 2008 15:25)
Re: O nas :-)
Taky něco přihodím. Možná někdo znáte stránku, ze které budu úlohy čerpat, ale to nevadí, ti kteří neznají, a? si započítají :-)
Petr Zaspal
Petr jezdí do školy autobusem, který odjíždí ze zastávky v 7:20. Z domova obvykle vychází v 7:00. Dnes se ale zpozdil a proto šel 1,2x rychleji. Na zastávku přišel o 4 minuty později než obvykle a autobus byl již dvě minuty pryč. V kolik hodin se dnes Petr vypravil z domova?
EDIT: Úloha je značně jednoduchá, sám jsem si jí teď bleskurychle vyřešil, ale i tak je to dobrá zábava na chvíli :-)
oo^0 = 1
Offline
#143 09. 07. 2008 16:22 — Editoval Chrpa (09. 07. 2008 16:24)
Re: O nas :-)
↑ ttopi:
Na zastávku přišel v 7 hodin 22 minut (20 + 4 - 2 = 22)
Normálně mu cesta trvala 18 minut. (20 - 2 = 18)
Protože šel 1,2 x rychleji, tak mu cesta tentokrát trvala 1,2 x kratší čas tj. 18/1,2 = 15 minut
Protože přišel na zastávku v 7 hodin 22 minut, pak z domova vyšel 7:22 - 15 = 7 hodin 07 minut
Offline
#144 09. 07. 2008 16:26 — Editoval ttopi (09. 07. 2008 16:30)
Re: O nas :-)
↑ Chrpa:
Uznávám, moc lehký, to bylo na rozcvičku :-)
Další:
Oslava narozenin
Ondřej vypočítává Vojtovi, kolik příbuzných se sešlo na oslavě jeho narozenin:
2 otcové, 2 matky, 2 synové, 1 dcera, 2 ženatí muži, 2 vdané ženy, 1 sestra, 1 bratr, 1 tchán, 1 tchýně, 1 dědeček, 1 babička, 1 snacha, 2 vnoučata. Kolik tam bylo lidí?
Manželské páry
Petr, Pavel a Ivan a jejich manželky Ivana, Alena a Jana mají dohromady 151 let. Každý muž je starší o 5 let než jeho manželka. Petr je o rok starší než Alena, Ivana a Petr mají dohromady 48 let, Ivana a Ivan 52 let. Určete manželské páry a stáří jednotlivých osob.
Veslařské závody
Dva sportovci se připravovali na veslařské závody, a proto trénovali. Jeden trénoval na řece. Vesloval jednou proti proudu, jednou po proudu. Druhý vesloval na téže vzdálenosti na jezeře. Oba veslaři byli na stejné úrovni a vynakládali tutéž energii, vyvíjeli tutéž rychlost po celou dobu tréninku. (kdyby byli oba na řece nebo na jezeře, plavali by stále vedle sebe a do cíle by přišli současně.) Kdo byl v cíli dřív?
Věk fotbalisty
Průměrný věk mužstva hráčů kopané je 22 let. Po odchodu zraněného hráče je průměrný věk zbylých hráčů 21 let. Kolik roků je zraněnému hráči?
oo^0 = 1
Offline
#148 09. 07. 2008 19:33
Re: O nas :-)
↑ Chrpa:
Tam je problém v tom, že se tam vyskytuje "kdyby se dožil" , "kdy bude" ... Z toho se to těžko počítá. 86 není celočíselně dělitelná 3, takže se s tím těžkce pracuje...
Spíš bych chtěl najít chybu v mé úvaze :-)
oo^0 = 1
Offline
#149 09. 07. 2008 19:35 — Editoval Chrpa (09. 07. 2008 19:38)
Re: O nas :-)
Závody
označme: v - rychlost veslaře na jezeře
vr - rychlost proudu řeky
rychlost veslaře na řece bude - po proudu: v + vp
proti proudu v - vp
Průměrná rychlost veslaře na řece bude: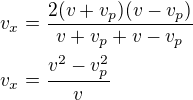
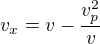
Rychlost veslaře na jezeře je 

V cíli bude dříve veslař na jezeře
Offline
#150 09. 07. 2008 21:24 — Editoval ttopi (09. 07. 2008 21:26)
Re: O nas :-)
Možná už někdo zná tyto stránky. Je tu spousta dobrých relaxačních her s opravdu širokou škálou možností nastavení. Opravdu si to projeďte.
Je tam třeba hra, kde máte odhadovat těžiště, střed kružnice opsané, nebo doplňovat čísla (přirozená, komplexní...) mezi operační znaménka tak, aby byl správný výsledek a spousta dalších jiných her.
Tady to je, příjemnou zábavu :-)
1.stránka - tady si dejte třeba "Triangular shoot"
a
2.stránka - tady zkuste "Arithmetic tables" s nějakým těžším nastavením.
Opravdu se u toho dá pobavit apopřemejšlet, což vám procvičí mozek :-)
oo^0 = 1
Offline