Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Ekvivalence množin (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 06. 2011 10:47 — Editoval Sulfan (27. 06. 2011 11:04)
Ekvivalence množin
Ahoj,
chtěl bych se zeptat, co přesně znamená, že jsou dvě množiny ekvivalentní. Příkládám definici ze skript:
To znamená, že každá funkce (zobrazení), která je prostá a vzory jsou v množině A a obrazy jsou v množině B, pak pro ně platí A~B?
Například:
 , potom
, potom 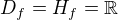
nebo
 , potom je množina
, potom je množina 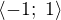 ekvivalentní s množinou
ekvivalentní s množinou  ?
?A následně, pokud máme zjistit, zda jsou dvě množiny ekvivalentní, pak stačí najít libovolnou funkci, která bude mít
 a
a 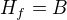 ?
?Děkuji za odpověď.
Edit: špatné násobky pi
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 27. 06. 2011 11:02 — Editoval musixx (27. 06. 2011 11:07)
Re: Ekvivalence množin
Trochu skripta hrající si se slovíčky, řekl bych, a pomíjející to, co vlastně chceme popsat.
Je rozdíl mezi
-- zobrazením množiny A do množiny B
-- zobrazením množiny A na množinu B
-- zobrazením z množiny A do množiny B
-- zobrazením z množiny A na množinu B
V prvním a druhém má každý prvek z A nějaký obraz, ve třetím a čtvrtém tomu tak být nemusí.
Ve druhém a čtvrtém má každý prvek z B nějaký vzor, v prvním a třetím tomu tak být nemusí.
Injektivní zobrazení na množinu je tedy bijekce, a to je také obvyklá (neslovíčkařící a na první pohled symetrická) definice ekvivalentních množin.
EDIT: Proto jsou tebou uvedené příklady opravdu důkazy ekvivalencí množin, neboť jde na uvažovaných definičních oborech o bijekce. Obecně je teda třeba najít nejen nějaké zobrazení jedné množiny na druhou, ale bijektivní zobrazení.
Offline
#3 27. 06. 2011 11:15
Re: Ekvivalence množin
↑ musixx: Máte naprostou pravdu s těmi předložkami "na" a "do". V jiných definicích ve skriptech se používá jiného slova a já si toho ani nevšiml. Nevím, jestli jsem všechny ty informace pochopil správně, ale zeptám se:
Pokud tedy zobrazujeme do množiny, pak stačí vědět, že pro každý prvek z A najdeme jeho obraz, ale o obrazy se nestaráme.
Když zobrazujeme na množinu, pak to znamená surjektivitu? ("ke každému obrazu nalezneme vzor", ale dál se o vzory nestaráme)
Takže když je injektivní zobrazení zároveň bijektivní, pak jsou množiny ekvivalentní?
Jinak se omlouvám za zjednodušování a za neexaktnost, chci pochopit definici :D
Offline
#4 27. 06. 2011 11:46 — Editoval LukasM (27. 06. 2011 13:11)
Re: Ekvivalence množin
↑ Sulfan:
Já bych to možná trochu poupravil.
Pokud zobrazujeme množinu do množiny, pak víme, že pro každý prvek z A najdeme jeho obraz v B, ale o obrazy se "nestaráme" (v tom smyslu, že nehlídáme jestli každý prvek B je obrazek něčeho z A).
Např. sin(x) je zobrazení R do R, ale ne R na R.
Pokud zobrazujeme na množinu, znamená to surjektivitu, to ano. Ovšem formulace "ke každému obrazu najdeme vzor" mi připadá jako tautologie. Surjektivita znamená, že každý prvek množiny B je obrazem nějakého prvku z množiny A.
Pokud je zobrazení bijektivní (v tom už je schovaná injektivita, takže netřeba ji ještě požadovat zvlášť), pak jsou množiny ekvivalentní.
Jak píše (srozumitelněji) ↑ musixx:, množiny jsou ekvivalentní, pokud existuje bijekce jedné množiny na druhou. Tedy pokud jde najít způsob, aby každý prvek z jedné množiny držel za ručičku právě jeden prvek z té druhé.
Edit: Jinak tobě jistě známý asistent Pytlíček považoval rozdíl mezi pojmy zobrazení množiny/z množiny za naprosto zřejmý, taky jsem v tom měl chvíli guláš :-)
Snad jsem v tom výkladu neplácl něco špatně, kolega musixx to jistě zkontroluje. Děkuji.
Offline
#5 27. 06. 2011 12:19 — Editoval Rumburak (27. 06. 2011 14:45)
Re: Ekvivalence množin
↑ Sulfan:
Kolega ↑ musixx: momentálně není připojen, tak snad nebude vadit, když se pokusím na dotazy odpovědět místo něho.
Předpokládejme, že f je zobrazení (funkce).
I. Výrok "f zobrazuje A do B" znamená, že pro každé  je
je 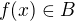 . Tím definice končí - pro její naplnění už žádné další
. Tím definice končí - pro její naplnění už žádné další
vlastnosti množin A, B ani funkce f nejsou potřeba.
II. Výrok "f zobrazuje A na B" znamená, že pro každé  je
je 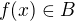 (jako prve), ale k tomu ještě něco navíc , a sice
(jako prve), ale k tomu ještě něco navíc , a sice
že pro každé  existuje
existuje  tak, že
tak, že 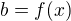 . Tento případ není v rozporu s případem I, ale je jeho zvláštní (speciální)
. Tento případ není v rozporu s případem I, ale je jeho zvláštní (speciální)
variantou.
Místo "f zobrazuje A na B" se též říká "f zobrazuje A do B surjektivně" , "zobrazení f: A do B je surjekce" a podobně .
Ale aby se v těchto úvahách neutopila podstata ekvivalence množin, uveďme příklad.
Máme na stole hromadu příborových nožů (považujme ji za množinu N) a hromadu vidliček (považujme ji za množinu V) . Chceme zjistit,
zda je vidliček stejný počet jako nožů. Můžeme samožřejmě spočítat nože i vidličky a oba výsledky porovnat. Ale pokud nás zajímá pouze
vzájemné porovnání těchto čísel a ne čísla sama, pak můžeme postupovat i tak, že
(1) vezmeme jeden nůž z hromady nožů a jednu vidličku z hromady vidliček a dvojici odložíme stranou,
(2) krok (1) provádáme tak dlouho, dokud některá z obou hromad není vyčerpána.
Jistě není třeba rozebírat, jak a k jakým závěrům můžeme na základě tohoto algoritmu dospět. Pouze uvedu to, že opakováním kroku (1)
do vyčerpání některé z hromad vlastně konstruujeme jakési zobrazení (obecně z množiny N do množiny V resp. naopak, podle toho,
zda v odložené dvojici považujeme za její první prvek vžy nůž nebo vždy vidličku), toto zobrazení je zřejmě injektivní. Případ, kdy dojde
k vyčerpání obou hromad zároveň, znamená, že takto sestrojené zobrazení je dokonce bijekcí N na V (resp. V na N).
Offline
#6 27. 06. 2011 13:02
Re: Ekvivalence množin
↑ Rumburak:↑ LukasM: díky oběma! :) , myslím, že jsem to všechno pochopil včetně dodatečných pojmů.
Offline
#7 27. 06. 2011 13:12
Re: Ekvivalence množin
Děkuji za další příklady i jiné formulace stále toho téhož. Jistě jsou užitečné.
Osobně termín "zobrazení na množinu" nepoužívám, užívám pouze "zobrazení do" a případnou surjektivitu extra zmíním stejně, jak píše ↑ Rumburak: ("místo 'f zobrazuje A na B' se též říká 'f zobrazuje A do B surjektivně'"). To "na" se dá snadno přeslechnout a i přeřeknout a většinou je podstata tvrzení jinde, než ve slovíčkaření do/na.
Termín "zobrazení z množiny" (tzv. parciální zobrazení) bez nějakého dalšího explicitního upozornění je snad ještě horší případ, použití bych viděl tak maximálně třikrát za deset let, pak už je to na blázinec.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Ekvivalence množin (TOTO TÉMA JE VYŘEŠENÉ)
