Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 28. 06. 2011 18:13 — Editoval ((:-)) (12. 07. 2011 00:47)
Re: limita
↑ rimer:
Ako radí Halogan:
Použiješ vzťah  . U Teba je
. U Teba je ![kopírovat do textarea $a = \sqrt[3]{x}$](/mathtex/85/8582c3013cebb3665b12c9dbf82ab2cf.gif) a
a 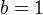 , potrebuješ vytvoriť
, potrebuješ vytvoriť 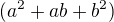 a potom rozšíriť týmto výrazom daný zlomok.
a potom rozšíriť týmto výrazom daný zlomok.
Súčasne ešte rozšíriš výrazom 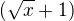 , aby si odstránil v menovateli pôvodný výraz s druhou odmocninou.
, aby si odstránil v menovateli pôvodný výraz s druhou odmocninou.
V čitateli aj menovateli vznikne výraz 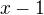 , ktorým môžeš zjednodušiť, lebo určite
, ktorým môžeš zjednodušiť, lebo určite 
Vyrátať potom limitu je už jahoda... :-)
Offline

![kopírovat do textarea $\lim_{x\to 1}\frac{\sqrt[3]{x}-1}{\sqrt x-1}$](/mathtex/7c/7ce93277f1da58e671f172256af06aa6.gif)
![kopírovat do textarea $\sqrt[6]{x} = t$](/mathtex/ca/caf4c194fd1ff28dc24fb00ec29dbb02.gif) (potom bude
(potom bude ![kopírovat do textarea $\sqrt[3]{x} = t^2$](/mathtex/9d/9da4ca49fb083a19a44fb4c01ca395bd.gif) ,
, 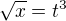 ) a větou o limitě složené funkce.
) a větou o limitě složené funkce.![kopírovat do textarea $\frac{\sqrt[3]{x}-1}{\sqrt x-1} = \frac{(\sqrt[3]{x}-1)\color{red}(\sqrt[3]{x})^2 + \sqrt[3]{x} + 1)\color{blue}(\sqrt x+1)}{(\sqrt x-1)\color{red}(\sqrt[3]{x})^2 + \sqrt[3]{x} + 1)\color{blue}(\sqrt x+1)}=\frac{(x-1)\color{blue}(\sqrt x+1)}{(x-1)\color{red}(\sqrt[3]{x})^2 + \sqrt[3]{x} + 1)}$](/mathtex/79/79be0f405b77e6a44bf6ad6abf4780c1.gif)