Matematické Fórum

kratajirka · 29. 06. 2011 22:24

Dobrý den, chtěl bych poradit s jedním příkladem, který sem dostal u příjímaček na VŠE.
jedná se o: Mezi kořeny kvadratické rovnice 2x^2-7x-4=0 vložte dvě čísla tak, aby spolu s těmito kořeny vznikly první čtyři členy geometrické posloupnosti. Součet vložených čísel je....
Řešením příkladu je -1. Může mi někdo poradit? po mnoha pokusech sem se nikdy k -1 nedostal. Děkuji

Hanis · 29. 06. 2011 22:25

Nejprve musíš vyřešit tu kvadratickou rovnici.

standyk

↑ kratajirka:

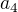Najprv si urči korene kvadratickej rovnice. Tie korene budú $a_1$ a $a_4$ geometrickej postupnosti.
Potom použi vzorec: 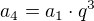$a_4=a_1\cdot q^3$ z toho dostávaš: $q=\sqrt[3]{\frac{a_4}{a_1}}$
Pomocou $q$ už ľahko dopočítaš 2. a 3. člen tejto postupnosti.

Vzniknú ti 2 postupnosti. Jedna rastúca a druhá klesajúca. Výsledný súčet to ale neovplyvní.

kratajirka · 29. 06. 2011 22:27

↑ Hanis:
(x-4)(x+1/2)=0 pokud se nepletu....

Hanis · 29. 06. 2011 22:31

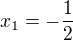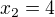paráda, kořeny jsou teda $x_1=-\frac12$ a $x_2=4$ , zbytek ti už poradil kolega ↑ standyk:

kratajirka · 29. 06. 2011 22:41

↑ Hanis:
to bych pochopil, ale já prostě nevim jak dál... a1 budiž -1/2 a a4=4....vložit mezi to 2 členy aby byl jejich součet -1? já prostě nevim...

standyk · 29. 06. 2011 22:44

↑ kratajirka:

Tuto ↑ standyk: som ti napísal ako zistíš kvocient geometrickej postupnosti. Keď ho zistíš, použiješ vzorec: 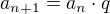$a_{n+1}=a_{n}\cdot q$ aby si určila druhý a tretí člen. Potom ich jednoducho sčítaš.

((:-)) · 29. 06. 2011 22:50 — Editoval ((:-)) (29. 06. 2011 22:55)

↑ kratajirka:

Autor skryl část textu. Zobrazit/skrýt!

kratajirka · 29. 06. 2011 22:51

↑ standyk:
aaaaj tady nejde o to že bych byl tak blbý a nevzdělaný a nevěděl vzroce - to jsem věděl ty co si zde napsal ae já jsem si neuvědomil jednu věc a to že je vždy (q) na xtou a ne q na xtou tudíž bude (-2)^2 a ne -2^2....to je moje hlouposta a zbytečně sem ztratil 5 bodů... omlouvám se za otravování ae vážně mi to nedalo spát kde je chyba a ono to je v tomto a ne ve vzorcích... Děkuji za trpělivost! :)

standyk

↑ kratajirka:

Nikto si nemyslí že si blbý! A ani nikoho neotravuješ. Na to je toto fórum a každý tu je dobrovoľne takže sme radi že už je jasno :)

Označ prosím ťa tému za vyriešenú.

kratajirka · 29. 06. 2011 22:59

↑ standyk:
ano ano...děkuji za váš strávený čas i když ve výsledku bylo vše jinak. :) přeji krásný zbytek dne :)

Waxion · 03. 06. 2016 22:55

můžete mi někdo vysvětlit, jak jste dostali k a4 prosím?

Akojeto · 03. 06. 2016 23:01

↑ Waxion:

Je to v príspevku #3.

Waxion · 03. 06. 2016 23:08

↑ Akojeto:
tam je to akorát napsané, ale není to vysvetlené a já jsem dost natvrdlý abych to chápal -.-

Akojeto

↑ Waxion:

Veď to je v zadaní - medzi korene kvadratickej rovnice vložte ...

To znamená, že 1. člen je $a_1$ potom sú členy. a2, a3 ktoré hľadáš a posledný 4. člen $a_4$ .

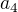To na kraji sú tie korene...

Čítaj poriadne a kresli si prečítané. Neviem, čo na tomto treba vysvetľovať, stačí si to znázorniť.

Waxion · 03. 06. 2016 23:22

↑ Akojeto:
Aha, uz to mám. Vůbec jsem nekoukal na zadaní.
Děkuji za trpělivost

Akojeto · 03. 06. 2016 23:45

↑ Waxion:

:-)

marnes · 25. 03. 2021 09:53 — Editoval marnes (25. 03. 2021 09:53)

↑ Prettyisdash:
1) vytvoř si pomocí venovych diagramů čtyři disjunktní podmnožiny
2) ze zadaných údajů vytvoř rovnice
3) určí počet prvků jednotlivých podmnožin
4) pak půjde teprve odpovědět na otázku

5) bylo by dobré do vlastního nového tématu

Matematické Fórum

#1 29. 06. 2011 22:24

Geometrická posloupnost pomocí kvadratické rovnice.

#2 29. 06. 2011 22:25

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#3 29. 06. 2011 22:27 — Editoval standyk (29. 06. 2011 22:28)

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#4 29. 06. 2011 22:27

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#5 29. 06. 2011 22:31

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#6 29. 06. 2011 22:41

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#7 29. 06. 2011 22:44

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#8 29. 06. 2011 22:50 — Editoval ((:-)) (29. 06. 2011 22:55)

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#9 29. 06. 2011 22:51

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#10 29. 06. 2011 22:55 — Editoval standyk (29. 06. 2011 22:56)

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#11 29. 06. 2011 22:59

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#12 03. 06. 2016 22:55

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#13 03. 06. 2016 23:01

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#14 03. 06. 2016 23:08

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#15 03. 06. 2016 23:19 — Editoval Akojeto (03. 06. 2016 23:20)

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#16 03. 06. 2016 23:22

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#17 03. 06. 2016 23:45

Re: Geometrická posloupnost pomocí kvadratické rovnice.

#18 25. 03. 2021 09:32 Příspěvek uživatele Prettyisdash byl skryt uživatelem Prettyisdash.

#19 25. 03. 2021 09:53 — Editoval marnes (25. 03. 2021 09:53)

Re: Geometrická posloupnost pomocí kvadratické rovnice.

Zápatí