Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
 be reals satisfying
be reals satisfying  and
and ![kopírovat do textarea $f, g \colon [0, 1] \to [0, \infty)$](/mathtex/8a/8a7129f9143ec909e758bd283762cca4.gif) continuous functions satisfying
continuous functions satisfying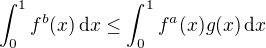 .
.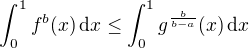 .
.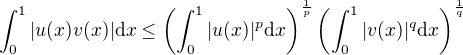 which holds for all
which holds for all 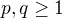 satisfying
satisfying 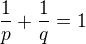 and
and 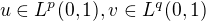 .
.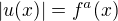 ,
, 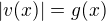 ,
, 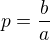 and
and 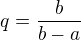 we may write
we may write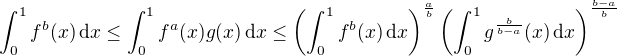 .
.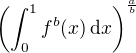 yields
yields ,
,