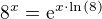Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integrál - per partes (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 07. 2011 19:13
- mischell90

- Příspěvky: 117
- Reputace: 0
integrál - per partes
Ahoj, můžu se prosím zeptat, jak byste zintegrovali integrál 8^x/ln(8)?
Offline
- (téma jako vyřešené označil(a) mischell90)
#2 16. 07. 2011 19:28
Offline
#3 16. 07. 2011 19:31
Re: integrál - per partes
A pak bych nepoužil per partes ale substituci y = x ln 8. Ve výsledku pak z toho vznikne (ln 8)^2 ve jmenovateli.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#4 17. 07. 2011 11:56 — Editoval mischell90 (17. 07. 2011 12:02)
- mischell90

- Příspěvky: 117
- Reputace: 0
Re: integrál - per partes
pořád mi nějak nevychází..derivace xln(8) = ln(8) nebo se mýlím? takže mi vychází integrál z e^t*dt/ln(8) a teď nevím co s tím ln(8) ve jmenovateli
Offline
#5 17. 07. 2011 12:21
Re: integrál - per partes
↑ mischell90:
Podle rady od ↑ Oxyd: by ti mělo ve jmenovateli vyjít 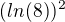 , ne
, ne 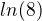 .
.
A co s tím? No, čeho jsi využila při tom derivování 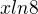 ? Proč to jde takhle zderivovat? Jak závisí hodnota
? Proč to jde takhle zderivovat? Jak závisí hodnota 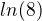 na té neznámé?
na té neznámé?
Offline
#6 17. 07. 2011 12:24
- mischell90

- Příspěvky: 117
- Reputace: 0
Re: integrál - per partes
no v tom zderivování mám právě zmatek..
Offline
#7 17. 07. 2011 12:26
Re: integrál - per partes
↑ mischell90:
Nemáš. Máš to zderivované dobře. Klíčem je si uvědomit, že 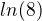 je konstanta. Jak při tom derivování, tak potom při výpočtu toho integrálu.
je konstanta. Jak při tom derivování, tak potom při výpočtu toho integrálu.
Offline
#10 17. 08. 2011 22:19
Re: integrál - per partes
↑ zwok_toon:
Ano. Když k je nějaká konstanta (její hodnota nezávisí na hodnotě x), tak platí 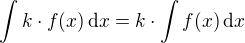 . Je to jedno ze základních tvrzení integrálního počtu.
. Je to jedno ze základních tvrzení integrálního počtu.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » integrál - per partes (TOTO TÉMA JE VYŘEŠENÉ)