Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Uzávěr spočetného sjednocení (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 07. 2011 20:05 — Editoval Olin (18. 07. 2011 20:07)
Uzávěr spočetného sjednocení
Nechť  je posloupnost podmnožin libovolného topologického prostoru. Dokažte, že
je posloupnost podmnožin libovolného topologického prostoru. Dokažte, že .
.
Offline
- (téma jako vyřešené označil(a) Olin)
#2 18. 07. 2011 20:57 — Editoval Pavel Brožek (18. 07. 2011 21:01)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Uzávěr spočetného sjednocení
Dokážu nejprve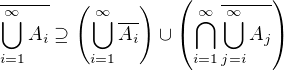 ,
,
k druhé části důkazu se případně vrátím později. (Zatím ji vymyšlenou nemám, předpokládám, že bude obtížnější.)
Offline
#3 20. 07. 2011 12:52
Re: Uzávěr spočetného sjednocení
Souhlasím. Uvedenou inklusi jsem dokazoval trochu stručněji:
Druhá inkluse mi vskutku připadla obtížnější.
Offline
#4 20. 07. 2011 14:13 — Editoval Rumburak (20. 07. 2011 14:15)
Re: Uzávěr spočetného sjednocení
↑ Olin: , ↑ Pavel Brožek:
Důkaz obrácené inkluse také není těžký :
Offline
#5 22. 07. 2011 00:10 — Editoval Olin (23. 07. 2011 12:51)
Re: Uzávěr spočetného sjednocení
↑ Rumburak:
Velmi pěkné, já jsem se při tomto důkazu nevyhnul topologickým úvahám.
Offline
#6 22. 07. 2011 09:54 — Editoval Rumburak (22. 07. 2011 10:14)
Re: Uzávěr spočetného sjednocení
↑ Olin:
Tvé řešení je také pěkné a stojí za to si ho zapamatovat. I v mém řešení jsou přítomny topologické úvahy, a sice hned v prvním řádku,
kde jsem využil skutečnosti, že operece uzávěru je konečně additivní. Holt jsme v topologii ...
(To sjednocení v podmínce (2) u Tebe zřejmě mělo probíhat od j = i. Já indexy i, j nerad používám vedle sebe,
protože při nižší hladině pozornosti se mi popletou buďto mezi sebou nebo s jedničkou. :-) )
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Uzávěr spočetného sjednocení (TOTO TÉMA JE VYŘEŠENÉ)
 . Pak nutně nastane alespoň jeden z následujících dvou případů:
. Pak nutně nastane alespoň jeden z následujících dvou případů:
 takové, že
takové, že  . Z definice uzávěru víme, že pro všechna okolí
. Z definice uzávěru víme, že pro všechna okolí  bodu x platí
bodu x platí 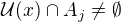 . Pro každé okolí bodu x proto také platí
. Pro každé okolí bodu x proto také platí  . To je opět definice uzávěru a máme tak
. To je opět definice uzávěru a máme tak  .
.
 je prvkem průniku, tudíž je prvkem každé množiny toho průniku:
je prvkem průniku, tudíž je prvkem každé množiny toho průniku: 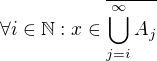 . Opět použiju definici uzávěru. Pro každé i a pro každé okolí
. Opět použiju definici uzávěru. Pro každé i a pro každé okolí  . Po záměně průniku a sjednocení
. Po záměně průniku a sjednocení  . Z toho víme, že existuje
. Z toho víme, že existuje  (závislé na i a
(závislé na i a 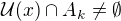 . Když zvětšíme jednu z množin v průniku, rozhodně tím nezpůsobíme, že by se najednou stal průnik prázdnou množinou:
. Když zvětšíme jednu z množin v průniku, rozhodně tím nezpůsobíme, že by se najednou stal průnik prázdnou množinou:  . Máme tedy opět to, co jsme chtěli,
. Máme tedy opět to, co jsme chtěli, 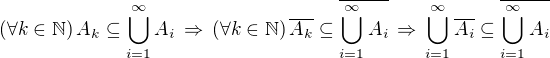
 ,
, je libovolné přirozené číslo. Potom
je libovolné přirozené číslo. Potom ,
,  ,
,  , obdržíme
, obdržíme  .
.  , neboli
, neboli 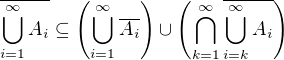 , QDE.
, QDE.
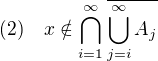 , (opraveno dle Rumburakova upozornění)
, (opraveno dle Rumburakova upozornění)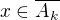 pro nějaké
pro nějaké 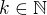 .
.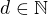 , že
, že 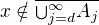 , tedy existuje takové okolí
, tedy existuje takové okolí 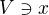 , že
, že  . Z (1) zase plyne
. Z (1) zase plyne  . Ukážeme, že
. Ukážeme, že 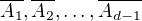 . Kdyby neleželo v žádné z těchto množin, znamenalo by to existenci okolí
. Kdyby neleželo v žádné z těchto množin, znamenalo by to existenci okolí 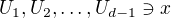 splňujících
splňujících  pro
pro  . V takovém případě by ovšem byla množina
. V takovém případě by ovšem byla množina 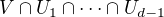 okolím
okolím 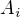 pro všechna
pro všechna  , což je spor s (1).
, což je spor s (1).