Matematické Fórum

terinkad · 19. 07. 2011 21:46

Ahoj vespolek, nebo dobrý den,
měla bych prosbu, jak spočítám průsečnici rovin? -987x-493y+116z+9042=0 a -1962x-1448y-565z+23122=0, Děkuju moc za pomoc

((:-)) · 19. 07. 2011 21:50 — Editoval ((:-)) (19. 07. 2011 22:04)

↑ terinkad:

Priamka v priestore sa dá určiť len parametricky alebo sa napíše, ktoré dve roviny sa v nej pretínajú.

Ja poznám len postup "hrubá sila".

1. Zvolím si dva bodyA,B, ktorých súradnice spĺňajú obidve rovnice (napríklad prvý bod x = 0 a potom dopočítam y a z bodu oboch priamok zo sústavy pre y a z, pre druhý bod zvolím napr. y = 0 a dorátam podobne x a z)

2. Zapíšem smerový vektor priamky napríklad ako B - A

3. Zapíšem parametrické vyjadrenie priamky

Pri Tvojich číslach by sa mi to nechcelo... + je možné, že tento postup nefunguje vždy.

terinkad · 19. 07. 2011 22:02

↑ ((:-)):

Zadání zní, přímka c je dána průsečnící těchto dvou rovin, ale já nevím, jak na to přijít, vím, že se dá zapsat parametricky....ale jak to udelat? díky moc za odpoved

((:-)) · 19. 07. 2011 22:08

↑ terinkad:

A netreba niečo robiť ďalej? Je tam napísané, že máš vyjadriť tú priamku parametricky?

xxMari · 19. 07. 2011 22:11 — Editoval xxMari (19. 07. 2011 22:12)

staci to dat do matice, jej hodnost je 2 a teda riesenie zadava priamku - vyjde 1 "parameter":)

petrkovar

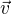Pro nalezení směrového vektoru průsečnice dvou rovin je šikovné použít vektorový součin normálových vektorů obou rovin. Souřadnice normálových vektorů snadno přečteme jako koeficienty u proměnných x, y a z. Označíme -li jeden normálový vektor $\vec{u}$ a druhý $\vec{v}$ , tak směrový vektor $\vec{s} = \vec{u} \times \vec{v}$ .
Tento postup selže pouze pokud jsou roviny rovnoběžné nebo splývají, neboť vektrový součin dvou rovnoběžných vektorů je nulový.

Edit: A souhlasím, že na některých školách se učí nalezení parametrického vyjádření výpočtem jistého determinantu. (mimochodem v tom determinantu lze vypozorovat výpočet kartézského součinu).

Edit2: A souhlasím i s tím, že řešení soustavy rovnic obou rovin je přímo parametrickým vyjádřením průsečnice (samozřejmě, pokud je hodnost soustavy 2 a taková průsečnice tedy existuje).

terinkad · 19. 07. 2011 22:15

↑ ((:-)):
Je tam napsane, ze mam urcit vzajemnou polohu primky a roviny, kde primka je zadana jako prusecnice techto rovin a ta druha rovina je zadana. Chces cele zadani?

rleg · 19. 07. 2011 22:16

↑ terinkad:
V zásadě to je jednoduché. Máš normálové vektory obou rovin a jejich vektorový součin ti dá směrový vektor průsečnice. Pak si zvolíš bod P [x,y,0] a dosadíš do obou rovnic rovin a vyřešíš to jako 2 rovnice o dvou neznámých. Takže máš bod a směrový vektor průsečnice a tím pádem můžeš napsat parametrickou rovnici průsečnice obou rovin.

xxMari · 19. 07. 2011 22:31

↑ terinkad:
ta rovina je zadana parametricky?

rughar · 21. 07. 2011 10:14

Omlouvám se, jestli toto řešení není totéž k tomu, co tu už někdo psal. Řekl bych ale že spíš ne.

1. Jako parametr si zvolím jednu ze souřadnic. Řekněme že parametr bude z.
2. Ze dvou rovnic rovin si vyjádřím neznámé x,y v závilosti na z

A tím máme hotové parametrické vyjádření přímky výjde něco jako

x = A*z + B
y = C*z + D
z = z

což můžeme přepsat do tvaru (pokud se nám nelíbí stejné označení souřadnice a parametru)

x = A*p + B
y = C*p + D
z = p

A,B,C,D budou nějaké konstanty které se získají z úpravy rovnic.

petrkovar · 21. 07. 2011 10:46

↑ rughar:Uvedený postup není obecný, musíme "odhadnout", zda nebude průsečnice kolmá na osu $z$ . V takovém případě nemůžeme zvolit za parametr $z$ . Méně zkušený počtář by se zasekl u soustavy rovnic, která nemá řešení a nevěděl by si rady.

Rumburak

↑ terinkad:

Nejprve shrnu zadání:
V 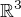$\mathbb{R}^3$ jsou dány tři roviny $\alpha$ , $\beta$ , $\gamma$ , z nichž $\alpha$ , $\beta$ jsou různoběžné a tedy se protínají v jisté přímce $p$ .
Máme za úkol vyšetřit vzájemnou polohu přímky $p$ s rovinou $\gamma$ .

Možný způsob řešení za předpokladu, že je zadání korektní, tj. že roviny $\alpha$ , $\beta$ jsou skutečně různoběžné
(což by se snadno ověřilo na základě lineární nezávislosti jejich normálových vektorů):

Hledáme společné body všech tří rovin (tj. jejich rovnice dáme do soustavy, kterou řešíme; každé její řešení
představuje jeden společný bod všech těchto tří rovin). Možné výsledky:

žádný společný bod ... ==> přímka $p$ je rovnoběžná s rovinou $\gamma$ a neleží v ní ,

právě jeden společný bod ... ==> přímka $p$ je různoběžná s rovinou $\gamma$ a protíná ji právě v tomto bodě,

více než jeden společný bod ... ==> přímka $p$ leží v rovině $\gamma$ .