Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 27. 08. 2011 21:30
Re: infinite series
Offline
#4 03. 10. 2011 16:20
Re: infinite series
Ahoj,
vase poznamky su zaujimave, no vsak to nie ja matematicky dokaz konvergencie postupnosti 
Tu vam dam jeden navod na riesenie tohto prikladu
Polozte  (ako Vak) a dokazte:
(ako Vak) a dokazte:
A z toho ze 
A na koniec ze  konverguje
konverguje
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 05. 10. 2011 13:49 — Editoval Marian (05. 10. 2011 13:50)
Re: infinite series
My solution of the convergence of the given sequence uses a different approach.
Offline
#6 05. 10. 2011 23:47
Re: infinite series
Akoze je tu vyssie uz jedno kompletne riesenie tak doplnujem aj to co som navrhol

konkluzia
Prirodzena otazka na doplnenie tohto problemu je:
kedy konverguje (diverguje)
 ?
?Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 07. 10. 2011 19:21 — Editoval Pavel (07. 10. 2011 19:25)
Re: infinite series
The convergence of the nested root expression can be shown by means of infinite series.
↑ vanok:
Konvergence resp. divergence výrazu
 je již kompletně vyřešena, viz zde
je již kompletně vyřešena, viz zdehttp://mathworld.wolfram.com/NestedRadical.html
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 09. 10. 2011 01:57
Re: infinite series
Hi Pavel,
I hope you realize that any problem was solved is of this type
But it may be interesant prove this result (Herschfeld's convergence theorem)
Quick comment:
In your demonstration you useful terms like

whose existence has not yet demonstrated.
Sincerely Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 09. 10. 2011 08:55
Re: infinite series
↑ vanok:
The existence of the (infinite) continued root is not the most important thing. The given sequence is monotone and positive and hence for the limit we can deduce only two essentially different cases: finite limit or infinite limit  . Using this fact, Pavel should only to rewritte some of the inequlaity signs
. Using this fact, Pavel should only to rewritte some of the inequlaity signs  to
to  . The rest holds true.
. The rest holds true.
Offline
#10 09. 10. 2011 12:07
Re: infinite series
Ahoj ↑ Marian:
Mathematics are an exact science and has little near is has to banish
Pavel little to give his own opinion and he does not need a spokesman
Sincerely Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 09. 10. 2011 14:04
Re: infinite series
↑ Marian::
It is you who must know him ["I know what is math"]
And respect also for the others
I repete:
Mathematics are an exact science and has little near is has to banish
Be modest
With all my respects
Sincerly Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 09. 10. 2011 21:47
Re: infinite series
↑ vanok:
1. Máš pravdu, existenci nekonečné odmocniny jsem ve svém důkaze neuvedl. Stačilo by shora odhadnout obecný člen  , který jsi definoval dříve, a to nekonečnou řadou, ke které jsem dospěl ve svém příspěvku, a navíc ukázat, že posloupnost
, který jsi definoval dříve, a to nekonečnou řadou, ke které jsem dospěl ve svém příspěvku, a navíc ukázat, že posloupnost  je rostoucí. To pak implikuje existenci nekonečné odmocniny jako limity posloupnosti
je rostoucí. To pak implikuje existenci nekonečné odmocniny jako limity posloupnosti  .
.
2. Marianova poznámka je naprosto namístě, k příspěvkům se může vyjádřovat kdokoliv a v jakémkoliv pořadí a není zde zapotřebí někoho vychovávat a určovat, kdo je nebo není čí mluvčí a kdo má nebo nemá mít svůj názor. Navíc Marian je jeden z nejlepších na tomto foru, takže si může dovolit tvrdit "I know what is math."
3. Nejsem zřejmě v angličtině tak zběhlý, abych rozuměl větě "Mathematics are an exact science and has little near is has to banish".
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#14 09. 10. 2011 22:35 — Editoval vanok (09. 10. 2011 22:42)
Re: infinite series
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 10. 10. 2011 00:54
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: infinite series
Jestli jsem to dobře pochopil, tak tu došlo k nedorozmění, že vanok měl ↑ zde: na mysli konečnost, ne samotnou existenci.
↑ Pavel:
Bodu 1 tvého příspěvku asi ne úplně rozumím. Mám z něho pocit, jako by stačilo k důkazu něco doplnit a tím by už byl v pořádku. Ale kdybychom k němu doplnili to, co píšeš, nebyl by už samotný důkaz ↑ zde: nadbytečný? Mně přijde, že by se hlavně měl důkaz pozměnit (ve smyslu bodu 1 tvého příspěvku), tak, abychom místo
dokazovali toto:
Offline
#16 10. 10. 2011 01:25 — Editoval Pavel (10. 10. 2011 01:36)
Re: infinite series
↑ Pavel Brožek:
Ano, máš pravdu, přesně tak jsem to navrhoval, tzn.
↑ vanok:
Kompletní důkaz Herschfeldovy věty najdeš zde:
http://pballew.net/1935Herschfeld.pdf
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#17 10. 10. 2011 02:22
Re: infinite series
Ahoj ↑ Pavel: a ↑ Pavel Brožek: a iny
Dakujem za zaujimave pdf.
Teraz po vymene nazorov z kolegami nemam ziadnu observaciu k Pavelomu rieseniu.
Najdolezitejsie pre matematiku je ze sme to vsetko spolupracou zdokonalili a vdaka tomu pdf mame naviac aj stvrte riesenie.
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

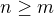 denote
denote 
 , where
, where  denotes the terms of the original sequence.
denotes the terms of the original sequence. ,
, 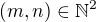 . Using the notation of
. Using the notation of  we obtain that
we obtain that there exists a positive integer
there exists a positive integer  such that for every
such that for every  the inequality
the inequality
 for
for  . From this we deduce that the sequence
. From this we deduce that the sequence  is Cauchy and thus converges to a finite value.
is Cauchy and thus converges to a finite value.
 pre
pre 

 cize
cize 

