Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » komplexní a komplexně sdružené číslo v jedné rovnici (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 08. 2011 13:04
komplexní a komplexně sdružené číslo v jedné rovnici
ahoj, když se dostanu v příkladu do situace, že mám  , jak mohu pokračovat dále?
, jak mohu pokračovat dále?
napadá mě jedině to, použít  a udělat z obou komplexních čísel absolutní hodnoty? řeší se to takhle? a nebo je ještě nějaký jiný způsob?
a udělat z obou komplexních čísel absolutní hodnoty? řeší se to takhle? a nebo je ještě nějaký jiný způsob?
Offline
- (téma jako vyřešené označil(a) r2d2)
#3 23. 08. 2011 13:29
Re: komplexní a komplexně sdružené číslo v jedné rovnici
↑ Jenda358:
no, to sice vím, ale nevím jak od sebe odečíst  ?
?
mohl bych to sice přepsat na  , ale to mám zase dvě proměnné v jedné rovnici? nanapsal by mi někdo náznak postupu jak dál?
, ale to mám zase dvě proměnné v jedné rovnici? nanapsal by mi někdo náznak postupu jak dál?
Offline
#5 23. 08. 2011 13:43
Re: komplexní a komplexně sdružené číslo v jedné rovnici
↑ Jenda358:díky moc, to jsem potřeboval, supr dík:-)
Offline
#6 23. 08. 2011 15:09 — Editoval r2d2 (23. 08. 2011 15:11)
Re: komplexní a komplexně sdružené číslo v jedné rovnici
tak pardon, mé zajásání bylo předčasné. já totiž nevím co jsem vlastně vypočítal:
rád bych sem tedy uvedl celý příklad:
Vyjádřit komplexní číslo ve tvaru z = a+bi
postupnými úpravami jsem se dostal k tomu, že 
a teď jak to dostat do tvaru z = a+bi. upravil jsem si to (viz. minulé příspěvky) na rovnici tu jsem rozepsal na
tu jsem rozepsal na a výsledek je:
a výsledek je:
ale napadla mě zásadní otázka. vypočítal jsem komplexní a nebo kopmlexně sdružené číslo. resp. vím že  ,
,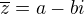 takže je to
takže je to
1)  a
a  a nebo je to
a nebo je to
2)  a
a 
fakt teď nevím?
Offline
#7 23. 08. 2011 15:29 — Editoval Phate (23. 08. 2011 15:29)
Re: komplexní a komplexně sdružené číslo v jedné rovnici
↑ r2d2:
par chybek:
1) a a b jsou realna cisla nemuzes tam plest zadne icka, asi jsi se nekde spletl
2) komplexne sdruzena cisla jsou vzdy podle osy x, takze celou cast maji stejnou a iamginarni se lisi o znamenko. Ty jsi jakesi a vypocital, tak proc mu menis znamenko?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#8 23. 08. 2011 15:55
Re: komplexní a komplexně sdružené číslo v jedné rovnici
Ano, a je reálná část a b je realny koeficient imaginární části, ale asi jsem to měl zapsat jinak - V TOMHLE MÁM TROCHU ZMATEK. já si jenom nejsem jistý jelikož jsem měl vyjádřit z, tak jaké je znaménko před b? a s tou změnou znaménka u 2 jsem se sekl to vidím.
takže a je realne cislo a b taky  bez i ale jako zápis použiju
bez i ale jako zápis použiju je to tak? Ale teď jde o to, jestli je toto výsledek a jestli z se náhodou nerovná
je to tak? Ale teď jde o to, jestli je toto výsledek a jestli z se náhodou nerovná 
Není mi to jasné protože jsem měl v jedné rovnici jak komplexní tak komplexně sdružené číslo. Vypočítal jsem sice realné čísla a, b ale to znaménko před b má platit pro to komplexní číslo a nebo pro komplexně sdružené?
Offline
#11 23. 08. 2011 16:19 — Editoval Rumburak (23. 08. 2011 16:22)
Re: komplexní a komplexně sdružené číslo v jedné rovnici
↑ r2d2:
Toto  JE výsledek (tj. řešení rovnice
JE výsledek (tj. řešení rovnice  ), protože bylo předpokládáno
), protože bylo předpokládáno  a vyšlo
a vyšlo
(správně a jednoznačně)  . Potom ovšem
. Potom ovšem  , ale to už není kořen oné rovnice.
, ale to už není kořen oné rovnice.
Jsou úlohy, v nichž výsledkem je uspořádaná dvojice 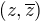 stejným právem jako
stejným právem jako  , avšak tato úloha k nim nepatří.
, avšak tato úloha k nim nepatří.
Offline
#12 23. 08. 2011 16:24
Re: komplexní a komplexně sdružené číslo v jedné rovnici
↑ Rumburak:díky moc, ale já si našel ve výsledcích, že se to má rovnat  , co s tím?
, co s tím?
Offline
#13 23. 08. 2011 16:27 — Editoval anes (23. 08. 2011 16:34)
Re: komplexní a komplexně sdružené číslo v jedné rovnici
↑ Rumburak:
Problém bude v
rád bych sem tedy uvedl celý příklad:
Vyjádřit komplexní číslo ve tvaru z = a+bi
postupnými úpravami jsem se dostal k tomu, že
↑ r2d2: Pokud není tvar zadání nějak extra hezký, tak je jednodušší nehrát si s tím a rovnou si to z rozepsat na re a im část. Čarováním se z jako celkem si moc nepomůžeš a snadno vyrobíš nějakou chybu (jak je vidět).
Pokud jsme vycházeli z  , tak je výsledek
, tak je výsledek  správný (nakonec není nic jednoduššího, než pro ověření dosadit).
správný (nakonec není nic jednoduššího, než pro ověření dosadit).
EDIT: Někde ses přehlíd/upsal a pak se to několikrát zkopírovalo.  a ne
a ne  , ale o to tady asi nejde.
, ale o to tady asi nejde.
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » komplexní a komplexně sdružené číslo v jedné rovnici (TOTO TÉMA JE VYŘEŠENÉ)






 , tak ti vyjde stejne vysledek, jen jine hodnoty
, tak ti vyjde stejne vysledek, jen jine hodnoty 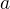 a
a 
 , je to tak správně?
, je to tak správně? a teď už se asi budu ptát hloupě: co dál s tím?
a teď už se asi budu ptát hloupě: co dál s tím? a
a 

 a vypadá to, že se rovnají. Ale snažím se přijít na to jak se dostat k výsledku z = 3 + i, který je u toho napsaný.(?)
a vypadá to, že se rovnají. Ale snažím se přijít na to jak se dostat k výsledku z = 3 + i, který je u toho napsaný.(?) a
a