Matematické Fórum

etchie · 31. 08. 2011 21:56

v teste z diferencialneho. a integ. poctu je zadanie:
Aku najmensiu vzdialenost moze mat bod $[x \sqrt{2};x], x\in\mathrm R$ od bodu $[0;6]$ ?
$a) \sqrt6 b) 2\sqrt6 c) 6 d) 6\sqrt2$

Spravnu odpoved sice viem zistit, ale sposobom ktory nema nic spolocne s diferencialnym a integralnym poctom. Ide o vylucovaciu metodu. Bod $[x \sqrt{2};x]$ je sucastou linearnej funkcie $y=\frac{x}{\sqrt2}$ . Z bodu [0;6] sa da nakreslit kruznica o polomere r, ktora by sa v jedinom bode dotykala priamky tvorenej $y=\frac{x}{\sqrt2}$ . Tento polomer r je teda najmensou hladanou vzdialenostou. Funckia $y=\frac{x}{\sqrt2}$ je v tomto bode dotycnicou ku kruznici a je teda kolma na polomer r v bode dotyku. Cize mame pravouhly trojuholnik s preponou na osi y o dlzke 6. Potrebujeme zistit dlzku odvesny, ktora je zhodna s r. Hned mozme vylucit riesenie d) pretoze odvesna v tomto trojuholniku nemoze byt dlhsia ako prepona. Riesenie c) tiez vypadava, pretoze to by mohla byt pravda iba v pripade, ze funkcia y = 0. Ak si dosadim do Pythagorovej vety dlzku podla a) tak druha odvesna ma dlzku $\sqrt{30}$ . 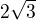Ak dosadim dlzku z b) tak druha odvesna bude mat dlzku $2\sqrt3$ Pravouhly trojuholnik ma rovnako dlhe odvesny iba ak je rovnoramenny, co by v tomto zadani bolo mozne iba ak by jedna odvesna lezala na funkcii y = x. Fukcia $y=\frac{x}{\sqrt2}$ ma mensie stupanie ako funkcia y = x, pretoze $\frac{1}{\sqrt2} < 1$ . Z toho vyplyva, ze ak na priamke nasej funkcie lezi pravouhly trojuholnik tak odvesna leziaca na priamke musi byt kratsia ako druha odvesna. 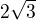Tuto podmienku splna pripad b) ked odvesna $2\sqrt3$ je mensia ako odvesna $2\sqrt6$ . Pre kontrolu: v pripade a) je $\sqrt{30}$ urcite viac ako $\sqrt{6}$ a teda podmienka splnena nie je.

a teraz k veci:
1. aky je normalny sposob riesenia tejto ulohy ? ak by sucastou zadania neboli moznosti a b c d, tak vylucovacia metoda samozrejme nefunguje
2. je pouzitie vylucovacej metody pre toto zadanie formalne spravne ? neurobil som niekde chybu ?

Napadlo ma, ze to mozem riesit ako 2 derivacie. Derivaciou linearnej funkcie y ziskam smernicu a presne tuto smernicu musi mat aj kruznica v bode dotyku s funkciou y. Alebo by sa to mozno dalo riesit ako sustava dvoch rovnic, kde riesenim je spolocny bod priamky a kruznice. Ak by som mal ten bod, kde sa priamka dotyka kruznice, tak uz nie je problem vyratat hladanu vzdialenost. Neviem to vsak zapisat do nejakeho vztahu, lebo je tam privela premennych (X, Y a R). Z pohladu derivacie je sice polomer r v rovnici kruznice konstanta a mohol by vypadnut, kedze bude zderivovany na nulu, ale z mojho pohladu je to neznama, ktoru hladam a nejak mi to cele nijako nezapada do seba.

dakujem za rady

zdenek1 · 31. 08. 2011 22:26

↑ etchie:
vzdálenost bodů
$d=\sqrt{(\sqrt2x)^2+(x-6)^2}$
hledáš minimum této funkce. Protože fce "odmocnina" je rostoucí v celém D_f, stačí ti najít minimum fce
$y=3x^2-12x+36$

zderivuješ a derivaci položíš rovnu nule -> máš extrém -> zkontroluješ, že je tam minimum.

etchie · 01. 09. 2011 11:40

↑ zdenek1:

uz mi to je jasnejsie.

ked vsak nad tym uvazujem dalej tak ma napadlo toto:
funkcia z prikladu hore je parabola a parabola ma iba jeden extrem a presne ten hladame na urcenie najmensej vzdialenosti.
povedzme ale, ze prvy bod nebude zadany linearnou funkciou, ale takou funkciou, ktora po vyjadreni vzdialenosti d a naslednej derivacii vytvori funkciu, ktora ma 2 lokalne extremy, povedzme lokalne minimum aj maximum. (neviem ci to vobec je mozne, mat vo vysledku nieco take)
ked tuto derivaciu polozim rovnu nule tak ziskam 2 vysledky - ale co vtedy vlastne ziskam ? o com by hovorili tieto 2 cisla ?

zdenek1 · 01. 09. 2011 11:46

↑ etchie:
tak bys měl nejmenší a největší vzdálenost.

etchie · 01. 09. 2011 15:56

↑ zdenek1:

teda to by bol pripad, kde riesime polohu pevne definovaneho bodu oproti bodu, ktory sa nachadza na elipse (kruznici)
vtedy derivacia bude mat 2 extremy, z ktorych viem urcit najmensiu a najvacsiu vzdialenost.

pre pripad elipsy/kruznice to teda musia byt vzdy 2 extremy. jedinou vynimkou by bol asi iba pripad, kedy stred kruznice je zaroven pevne definovanym druhym bodom.
vtedy by bolo extremov: ? - neviem kolko

ked si zadam do WolframAlpha derivaciu rovnice kruznice o polomere r=3: (sqrt(9-x^2))'
tak zo zobrazeneho grafu by sa asi dalo povedat, ze extremy nie su ziadne - ale nie som si ani trochu isty ako interpretovat ten graf ani co z toho vyplyva

jelena · 02. 09. 2011 09:26

Zdravím v tematu,

doufám, že nevnesu větší zmatek do tohoto celkem nepřehledného tématu.

1)

↑ etchie: - úvaha v 1. příspěvku se mi nezdá úplně v pořádku (ohledně jistoty zápisu funkce y=... lineární). O tom nic nevíme. Máme pouze jeden bod $[x \sqrt{2};x], x\in\mathrm R$ , který funkci náleží, předpis funkce není dán, ani naznačen.

V otázce je "Aku najmensiu vzdialenost moze mat bod..."

Úvaha, že vzdálenost od bodu $[0;6]$ se má hledat na kružnici se středem S $[0;6]$ , to už se mi zdá v pořádku. Potom sestavím předpis kružnice:

$x^2+(y-6)^2=r^2$ a pro zadaný bod $[x \sqrt{2};x]$ hledám takové $x$ , aby $r$ bylo minimální.

Po dosazení a po úpravě mám: $3x^2+12x+36=r^2$ nebo $(x-2)^2+8=\frac{r^2}{3}$ výraz nalevo bude minimální pro $x=2$ .

2) k příspěvku 5:

etchie napsal(a):
riesime polohu pevne definovaneho bodu oproti bodu, ktory sa nachadza na elipse (kruznici)...pre pripad elipsy/kruznice to teda musia byt vzdy 2 extremy. jedinou vynimkou by bol asi iba pripad, kedy stred kruznice je zaroven pevne definovanym druhym bodom.
vtedy by bolo extremov: ? - neviem kolko

Pro kružnici ostrý extrém žádný - nesouhlasilo by to s definici kružnice

Skoro OT:

etchie napsal(a):
1. aky je normalny sposob riesenia tejto ulohy ?

Co je normální?

↑ zdenek1:

Milý kolega Ondřej velmi nemá rad, když extrém kvadratické funkce hledáme pomoci derivace :-) Sleduji, že kolega Ondřej už postupně dosahuje pozice obdivuhodného kolegy Mariana minimálně v tom, co všechno nemá rad a čeho se mám vyvarovat.

Rumburak

↑ etchie:

Když křívka $k$ je spojitým obrazem uzavřeného intervalu a $C$ libovolně daný bod, potom obecně platí toto:

Funkce $f(X) := d (X, C)$ (vzdálenost bodu $X$ od bodu $C$ ) nabývá na množině $k$ jak svého absolutního minima, tak svého
absolutního maxima . (Platilo by to i pro každou jinou reálnou funkci $f$ definovanou a spojitou na křivce $k$ , což ale již pojmově přesahuje
rozsah látky SŠ.)

Příklad, kdy $k$ je oblouk kružnice, jejímž středem je právě bod $C$ , ukazuje, že bodů křívky, v nichž je abs. extrémů dosaženo, může být
nekonečně mnoho (extrémy ve zmíněm příkladu s obloukem kružnice a jejím středem však nejsou ostré).

I když by křivka $k$ nebyla obloukem kružnice, její tvar by mohl být i značně složitý, což pak by mohlo vést opět k nekonečnému množství
lokálních extrémů (dononce ostrých) a mohlo by jít i o extrémy absolutní. Křivka může mít i různé hroty, které velmi často bývají extrémálními
body nějaké funkce.

jelena · 02. 09. 2011 10:32

↑ Rumburak:

:-) děkuji a srdečný pozdrav.

Aby nedocházelo k nedorozumění - pro kružnici mluvím o extrému ostrém (což mi přišlo v praktickém použití "názornější"), proto jsem napsala "extrém žádný". Může to tak zůstat? Děkuji.

zdenek1 · 02. 09. 2011 10:33

↑ jelena:
Já také nehledám extrém kv. fce derivacemi. Ale já jsem pochopil "normální" v tématu dif. pocet jako že to chce přes derivace. Všimni si, že bez derivací to etchie zvládl sám.

jelena · 02. 09. 2011 10:47

↑ zdenek1:

:-) to jeho "zvládl sám" se mi tak úplně nepozdavalo, jinak bych nenapsala. A jinak - jen si tropím žerty, máš naprostou pravdu - měla bych nasadit vážný výraz a pokračovat v sekci Fyzika v převýchově kolegy TomaseP. (což je ovšem "riadná nuda" (c)). Také srdečný pozdrav :-)

Rumburak · 02. 09. 2011 10:55

↑ jelena:

Ahoj. :-) To slůvko "ostrý" bych tam raději doplnil, tedy "ostrý extrém žádný".

jelena · 02. 09. 2011 11:42

↑ Rumburak:

děkuji, doplněno.

etchie · 02. 09. 2011 16:22

↑ jelena:

no prave v tejto casti svojho vylucovacieho postupu som si bol isty, ze musi ist jedine o linearnu funkciu a to definovanu pre celu mnozinu R. kedze plati $x \in \mathrm R$ hoci je definovany iba jeden bod, tak pre kazde x je tymto zapisom zadane aj y; ten zapis chapem ako zadanie pomocou suradnic $[X;Y]$
akurat je to vymenene takze $X= x\sqrt{2}$ a $Y = x$
skor som si myslel ze chybu by som mohol mat niekde inde
v kazdom pripade ked pouzijem svoj oblubeny WolframAlpha a zadam [x sqrt(2); x] tak jedina mozna jeho intepretacia je linearna funckia.
bohuzial vsak Wolfram si mysli, ze tato funkcia ma vacsie stupanie ako 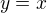$y = x$ . co je presny opak toho, co som pouzil v svojom vylucovacom postupe.

no a k slovu normalny: myslel som taky postup, najlepsie za pouzitia dif. a int. poctu, kde vysledok bude znamy bez ohladu na moznosti a b c d. staci totiz je aby dve z moznosti a b c d splnali moju podmienku "...odvesna leziaca na priamke musi byt kratsia ako druha odvesna" a uz sa vysledok neda jednoznacne urcit

jelena · 02. 09. 2011 17:03

↑ etchie:

děkuji, nepovídám, že Tvůj postup je nepoužitelný.

Původně jsem chtěla reagovat pouze na nezodpovězený dotaz z ↑ příspěvku 5:. Když jsem podrobně přečetla Tvůj postup, navrhla jsem svůj (není můj, je standardní).

Přišlo mi, že Tvůj postup obsahuje některé momenty, co ho zbytečně prodlužuji - například ověřovat, že bod může ležet jen a pouze na přímce a hledat předpis lineární funkce, potom úvahy atd. Můj postup je na 3 řádky i včetně nalezení hodnoty vzdálenosti $r$ . Ovšem nepoužívám žádné odhady, ani úvahy.

-------------------------------------------------------------------------------------

Pokud úloha byla z dif. počtu, tak samozřejmě platí postup kolegy ↑ zdenek1:.

etchie napsal(a):
v kazdom pripade ked pouzijem svoj oblubeny WolframAlpha a zadam [x sqrt(2); x] tak jedina mozna jeho intepretacia je linearna funckia.
bohuzial vsak Wolfram si mysli, ze tato funkcia ma vacsie stupanie ako y = x. co je presny opak toho, co som pouzil v svojom vylucovacom postupe.

Pokud předpokládáš, že bod leží na přímce $Y=kX+q$ (záměrně mám velké označení, aby se nepletlo), potom po dosazení zadaného bodu máš: $x=k\cdot x\sqrt2+q$ , $q=0$ , $k=\frac{1}{\sqrt2}$ , tedy předpisem je $y=\frac{1}{\sqrt2}x$ , není třeba křivdit oblíbenému Wolframu (on si myslí, že chceš nakreslit 2 různé funkce).

Je to tak v pořádku?

etchie · 04. 09. 2011 12:21

dakujem vsetkym za vysvetlenia a rady.

co som sa z nich naucil:
1. dva body v rovine, nech uz su zadane akymkolvek sposobom a nech lezia na priamke, elipse, ci inej funkcii, su vzdy len dvoma bodmi niekde v sustave [x,y]
2. na urcenie vzdalenosti medzi dvoma bodmi si VZDY vystacime so vztahom pre pravouhly trojuholnik
3. pomocu tohto vztahu teda zostavime rovnicu priebehu vzdialenosti $d=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$
4. funkciu zderivujeme a urcime lokalne extremy funkcie v miestach kde derivacia = 0
5a. ak je extrem jeden, tak urcite ide o minimalnu vzdialenost
5b. pri dvoch extremoch mame najskor asi minimalnu a maximalnu vzdialenost - ide o pripad, ked poloha aspon jedneho z bodov je na uzavretej krivke ako je kruznica, elipsa a podobne
5c. viem si predstavit druhy bod definovany ako rovnicu paraboly alebo sinusoidy a vtedy by bolo mozne mat viac ako jedno minimum
6. ak mame vo vysledku viac ako jeden extrem, tak to ci ide o minimum alebo maximum je mozne obecne povedat az ked dosadime hodnoty x (v miestach nulovej derivacie) do povodneho vzorca na urcenie vzdialenosti d

vyvstaly u mna vsak este otazky k niektorym veciam co boli spomenute v tejto teme:
- "extrem kvadratickej funkcie nehladat podla derivacie" - chapem to dobre, ze pri kvadratickej funkcii extrem nemusime hladat pomocou "tazkeho delostrelectva" a plytvat municiou a energiou, kedze kvadraticka funkcia ma extrem vzdy jeden jediny, a to vrchol paraboly kde suradnica $x=-\frac{b}{2a}$ ?
- este by som sa rad nieco dozvedel o extreme "ostrom" a "neostrom" (ani som nevedel, ze take mozu byt) nieco som si o tom pozeral na nete, ale nic mi to nehovorilo

↑ jelena:
dakujem tiez za vysvetlenie ohladom WolframAlpha

zdenek1 · 04. 09. 2011 13:36

↑ etchie:

- "extrem kvadratickej funkcie nehladat podla derivacie" - chapem to dobre, ze pri kvadratickej funkcii extrem nemusime hladat pomocou "tazkeho delostrelectva" a plytvat municiou a energiou, kedze kvadraticka funkcia ma extrem vzdy jeden jediny, a to vrchol paraboly kde suradnica $x=-\frac{b}{2a}$ ?

ano, to chápeš naprosto správně.
jen doplním, že někteří jedinci si odmítají i pamatovat ten vztah, a doplňují na čtverec stylem
$y=x^2+2x-1=x^2+2x+1-2=(x+1)^2-2\ \Rightarrow\ V[-1;-2]$

jelena · 04. 09. 2011 15:00

↑ etchie:

děkuji. Ještě k otázkám:

5c. viem si predstavit druhy bod definovany ako rovnicu paraboly alebo sinusoidy a vtedy by bolo mozne mat viac ako jedno minimum

Upřesní, prosím, co je druhý bod?

Pokud posuzuji vzdálenost od bodu ke křivce, tak mohu mít speciální polohu tohoto bodu vzhledem ke křivce - pokud je na ose souměrnosti křivky (nebo na průsečíku os). Potom mám alespoň 2 body na křivce se stejnou vzdálenosti. To souvisí i s pojmem "ostrý extrém" - to je podle definice, že každý další bod je vzdálen více (pokud je ostré minimum) nebo méně (pokud je ostré maximum). V definici vidíme jen znaménko $<$ nebo $>$

"Jen" extrém považujeme i takovou situaci, pokud je každý další bod křivky vzdálen stejně nebo více od zadaného bodu (potom je to minimum) nebo pokud je vzdálen stejně nebo méně - je to maximum. Důležití je slovo stejně - v definici vidíme znaménko 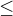$\leq$ nebo $\geq$ .

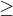↑ zdenek1:

nepamatuji ten vztah (je těžký :-) - také doplňuji na čtverec - ale dělení 2 je také těžké :-). Děkuji za kontrolu kolegy, snad jsme již nic nevynechali.

etchie · 04. 09. 2011 16:08 — Editoval etchie (04. 09. 2011 17:53)

↑ jelena:

k bodu 5c som to myslel tak, ze bod A je definovany napriklad ako $[\frac{\pi}{4};\frac{1}{5}]$ a bod B $[x;sin(x)]$
pripadne druha situacia kde je bod B definovany funkciou paraboly a pevny bod A umiestneny niekde v strede sumernosti krivky - presne na takuto situaciu "stred sumernosti" som myslel

a riesenim oboch by boli 2 extremy - lokalne minima ("neostre", kedze su 2 rovnake)

jelena · 04. 09. 2011 21:48

↑ etchie:

děkuji, už je to jasné - v případě bodu A - bod není nějak "speciálně" umístěn ve vztahu k sinusoidě (tedy vyšetření minimální vzdálenosti se provede přes hledání extrému). Druhá situace, že "pevný bod" je na ose souměrnosti vyšetřované křivky - to jsme také rozebrali.

Už jsme hodně daleko od původního zadání :-) Snad se bude hodit i tato sbírka slovních úloh s využitím dif. počtu - pro zpestření úloh na vzdálenost.

Ať se vede.

Matematické Fórum

#1 31. 08. 2011 21:56

diferencialny a integralny pocet - slovna uloha

#2 31. 08. 2011 22:26

Re: diferencialny a integralny pocet - slovna uloha

#3 01. 09. 2011 11:40

Re: diferencialny a integralny pocet - slovna uloha

#4 01. 09. 2011 11:46

Re: diferencialny a integralny pocet - slovna uloha

#5 01. 09. 2011 15:56

Re: diferencialny a integralny pocet - slovna uloha

#6 02. 09. 2011 09:26

Re: diferencialny a integralny pocet - slovna uloha

etchie napsal(a):

etchie napsal(a):

#7 02. 09. 2011 10:23 — Editoval Rumburak (02. 09. 2011 11:13)

Re: diferencialny a integralny pocet - slovna uloha

#8 02. 09. 2011 10:32

Re: diferencialny a integralny pocet - slovna uloha

#9 02. 09. 2011 10:33

Re: diferencialny a integralny pocet - slovna uloha

#10 02. 09. 2011 10:47

Re: diferencialny a integralny pocet - slovna uloha

#11 02. 09. 2011 10:55

Re: diferencialny a integralny pocet - slovna uloha

#12 02. 09. 2011 11:42

Re: diferencialny a integralny pocet - slovna uloha

#13 02. 09. 2011 16:22

Re: diferencialny a integralny pocet - slovna uloha

#14 02. 09. 2011 17:03

Re: diferencialny a integralny pocet - slovna uloha

etchie napsal(a):

#15 04. 09. 2011 12:21

Re: diferencialny a integralny pocet - slovna uloha

#16 04. 09. 2011 13:36

Re: diferencialny a integralny pocet - slovna uloha

#17 04. 09. 2011 15:00

Re: diferencialny a integralny pocet - slovna uloha

#18 04. 09. 2011 16:08 — Editoval etchie (04. 09. 2011 17:53)

Re: diferencialny a integralny pocet - slovna uloha

#19 04. 09. 2011 21:48

Re: diferencialny a integralny pocet - slovna uloha

Zápatí