Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 09. 2011 20:19
- matematik123

- Příspěvky: 125
- Reputace: 0
Zlomky
Dobrý den,
můžete mi, prosím, co nejdetailněji vysvětlit postup u následujících příkladů? Pokud řeším ten první, vznikne z něj zlomek?
Pokud v rovnici převedu dělení na opačnou stranu, stane se z něj násobení?
matematik amathér
Offline
- (téma jako nevyřešené označil(a) matematik123)
#3 03. 09. 2011 20:49
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Teď jej tady nemám, ale nejsem si jistý, že chápu tohle. Nemohl bys mi vysvětlit první krok? Proč je to písmeno zrovna dole? Ideální by bylo, kdybys rozepsal to dělení krok za krokem. 
matematik amathér
Offline
#4 03. 09. 2011 20:56
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Zlomky
k tomu už se nedá víc napsat, máš to tam rozepsané krok za krokem, maximálně můžu doplnit slovní komentář:
1.) Chci z rovnice 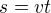 vyjádřit "
vyjádřit " "
"
2.) " " je na pravé straně násobeno "
" je na pravé straně násobeno " ", abych ho osamostatnil, použiju opačnou (odborně inverzní) operaci k násobení - dělení a obě strany rovnice vydělím "
", abych ho osamostatnil, použiju opačnou (odborně inverzní) operaci k násobení - dělení a obě strany rovnice vydělím " ". Dělení se úsporně zapisuje jako zlomek, je důležité si uvědomit, že
". Dělení se úsporně zapisuje jako zlomek, je důležité si uvědomit, že 
3.) Na pravé straně se nám " " pokrátí, což byla naše snaha a získáme výsledný vztah
" pokrátí, což byla naše snaha a získáme výsledný vztah 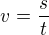
Abych to shrnul - vybereš si neznámou, a provádíš operace opačné s písmenky, které jsou na stejné straně. Postupuješ opačně, než když počítáš příklady. Obyčejně má přednost násobení a dělení před sčítáním a odčítáním, tady postupuješ od konce.
Je to tak srozumitelné?
Offline
#5 03. 09. 2011 21:06
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Omlouvám se, ale nemohl bys trochu rozvést tu dvojku? Chápu, proč to dělím t, ale ten postup mi není moc jasný.
matematik amathér
Offline
#6 03. 09. 2011 21:09
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Zlomky
↑ matematik123:
no na tom není těžkého, vezmu si levou stranu - to je  a vydělím jí
a vydělím jí - dostanu
- dostanu  - zjednodušeně (a někteří mi za to urvou uši) vezmu co mám napravo, udělám pod tím zlomkovou čáru a napíšu pod ní t :-)
- zjednodušeně (a někteří mi za to urvou uši) vezmu co mám napravo, udělám pod tím zlomkovou čáru a napíšu pod ní t :-)
a to samé s pravou stranou mám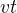 , vydělím
, vydělím  a dostanu
a dostanu 
Offline
#7 03. 09. 2011 21:32
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Zlomky
↑ matematik123: poznaš neco jako krateni zlomku? keď mame v zlomku súčin, napr.  a v čitateli a menovateli sú rovnaké pismenka alebo čisla, môžeme ich vykratiť - odstraniť ale iba keď su v súčine - napr
a v čitateli a menovateli sú rovnaké pismenka alebo čisla, môžeme ich vykratiť - odstraniť ale iba keď su v súčine - napr 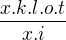 = ? ktore písmenka su rovnaké ? no predsa x - preto dostaneš z toho zlomku
= ? ktore písmenka su rovnaké ? no predsa x - preto dostaneš z toho zlomku 
chápeš?
Offline
#8 03. 09. 2011 21:35
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Super, díky moc, už je mi to jasné :)
matematik amathér
Offline
#9 03. 09. 2011 22:13
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Zlomky
↑ matematik123: neverim ze vďaka mne si nato prišiel?
Offline
#10 03. 09. 2011 22:33
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
A kvůli Hainosovi, to dělení mi nebylo moc jasné i když jsem tak trochu tušil, že se to dělá zhruba takhle.
matematik amathér
Offline
#11 04. 09. 2011 12:52
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Můžete mi ještě prosím vysvětlit první krok? Chápu, že je to kvůli tomu, že jsme chtěli odstranit zlomek a bylo výhodnější odstranit ten znak dole, protože je jen jeden. Ale nechápu, proč ten znak není i na druhé straně. Já osobně bych jej dal k tomu "u" a za "NI"
matematik amathér
Offline
#13 04. 09. 2011 13:16
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
A proč není i u toho "u"?
matematik amathér
Offline
#15 04. 09. 2011 13:21
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
OK, už je mi to myslím jasné.
matematik amathér
Offline
#16 04. 09. 2011 13:24
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Zlomky
↑ matematik123:
pro trénink si můžeš vzít tabulky, vybrat nějaký vzorec, zvolíš si neznámou a vyjádříš
pro kontrolu použij odkaz, napíš vzoreček ze kterého vyjadřuješ a za něj "for" a písmenko, např.:
Beispiel
Offline
#20 04. 09. 2011 18:41
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Nechápu ten třetí krok, mohl by prosím někdo to dělení 2t rozepsat detailněji?
matematik amathér
Offline
#21 04. 09. 2011 19:07
Re: Zlomky
S tou levou stranou se téměř nic nedělá -- jenom se „pod ni“ dá ten jmenovatel 2t.
U pravé strany platí 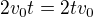 , protože na pořadí násobení nezáleží. Pak ji vydělím 2t a pokrátím zlomek:
, protože na pořadí násobení nezáleží. Pak ji vydělím 2t a pokrátím zlomek: 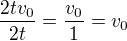 .
.
Dostanu tak rovnici 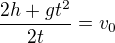 . Autor tohohle postupu si ještě přehodil strany rovnice, takže dostal
. Autor tohohle postupu si ještě přehodil strany rovnice, takže dostal  a pak dál upravoval pravou stranu.
a pak dál upravoval pravou stranu.
Nejdřív tu pravou stranu rozdělí na dva zlomky: Protože platí 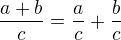 , tak se dá upravit
, tak se dá upravit 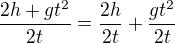 . Dál už je to jenom krácení -- v prvním zlomku se pokrátí dvojka a vznikne z toho
. Dál už je to jenom krácení -- v prvním zlomku se pokrátí dvojka a vznikne z toho  , ve druhém zlomku se zase pokrátí t (v čitateli je
, ve druhém zlomku se zase pokrátí t (v čitateli je  , takže když „jedno t seberu“, tak mi tam zůstane jenom
, takže když „jedno t seberu“, tak mi tam zůstane jenom  ) -- vznikne
) -- vznikne 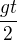 .
.
Jak už naznačil Hanis, platí 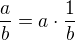 , takže podle toho můžu upravit
, takže podle toho můžu upravit  . To je zase násobení a na pořadí násobení nesejde, takže to můžu napsat jako
. To je zase násobení a na pořadí násobení nesejde, takže to můžu napsat jako 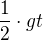 .
.
Celkem to dává ten výsledek, který si tu napsal.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#23 04. 09. 2011 21:42
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Bylo by velkou chybou kdybych napsal u toho posledního kroku nechal gt/2?
matematik amathér
Offline
#24 04. 09. 2011 21:46
Re: Zlomky
↑ matematik123:
Ne, nebylo. Je to v zásadě otázka toho, „jaký tvar se ti líbí“. V pohodě bys to mohl nechat na  -- už to je vyjádření
-- už to je vyjádření 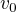 .
.
Je to otázka toho, co se ti víc líbí a s čím se ti bude lépe pracovat. (Na SŠ taky otázka toho, co už učitel považuje za „zjednodušený“ tvar a co nikoliv.)
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#25 04. 09. 2011 21:58
- matematik123

- Příspěvky: 125
- Reputace: 0
Re: Zlomky
Jasně, ten základní tvar je zbytečně složitý, ale ten úplně krok by mě sám od sebe nenapadl. Spokojil bych se s gt/2.
Tak díky za radu, konečně tomu začínám rozumět.
matematik amathér
Offline


 jinak by to vypadalo, kdyby se tam objevil součet
jinak by to vypadalo, kdyby se tam objevil součet