Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 09. 2011 21:06
Limita výrazu s třetí odmocninou
Ahoj.. Na vlastní pěst se učím limity, protože potřebuju nutně co nejdřív umět derivovat a integrovat a podobné legrácky.
(znáte to jak fyzika předbíhá matematiku :))
A zasekl jsem se u jednoho typu příkladů. Určitě se najde někdo kdo pomůže ne?![kopírovat do textarea $\lim_{x\to 1}\frac{\sqrt[3]{x}-1}{\sqrt x -1}$](/mathtex/32/32dfcfb4ecb566c062d2132df13ef792.gif)
Nevím jak se zbavovat těch třetích odmocnin. Resp. se mi s ničím ten jmenovatel nepokrátí, aby byl ten výraz pro tu jedničku definován a já mohl použít pravidlo o limitě dvou funkcí.
nebo třeba![kopírovat do textarea $\lim_{x\to 0}\frac{\sqrt[3]{x+ax}-1}{x}, a \in R$](/mathtex/48/4852be44fd59b028c1693552cc10cbcd.gif)
Tady vůbec nevím jak postupovat. Je to jakási limita s parametrem, že? Zase nevím co s tou odmocninou :)
Offline
- (téma jako vyřešené označil(a) SagiCZ)
#3 08. 09. 2011 00:20
Re: Limita výrazu s třetí odmocninou
Jestli můžu, já bych tady asi neváhal použít L'Hospitalovo pravidlo, mám za to, že je to přesně případ, kdy by se mělo používat - čitatel i jmenovatel je roven nule:![kopírovat do textarea $
\lim_{x \to 1} \frac{\sqrt[3]x-1}{\sqrt x-1} = \lim_{x \ to 1} \frac{\frac{1}{3\sqrt[3]{x^2}}}{\frac{1}{2\sqrt{x}}} = \lim_{x\to 1} \frac{2\sqrt{x}}{3\sqrt[3]{x^2}} = \frac{2\sqrt{1}}{3\sqrt[3]{1}} = \frac{2}{3}
$](/mathtex/ec/ec4d2f1b01245dbcb67786967b4ac1e1.gif)
Wolfram
wolfram mi výsledek potvrdil, takže to bude správně. :-)
Jinak u L'Hospitalova pravidla jde o to, že pokud je čitatel i jmenovatel rovný 0 nebo jsou oba rovny plus mínus nekonečnu, pak platí vztah:
Jestli ale neumí derivovat, tak se omlouvám za toto řešení, přijde mi ale nejsnazší. :-)
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 08. 09. 2011 09:33
Re: Limita výrazu s třetí odmocninou
found napsal(a):
Jinak u L'Hospitalova pravidla jde o to, že pokud je čitatel i jmenovatel rovný 0 nebo jsou oba rovny plus mínus nekonečnu, pak platí vztah:
Formulace těch předpokladů by mohly být přesnější, ale o to mi teď až tak nejde. Jde mi o to, že jeden důležitý předpoklad tam zcela chybí,
a sice předpoklad, že
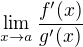 existuje .
existuje .
Offline
#5 08. 09. 2011 10:21
Re: Limita výrazu s třetí odmocninou
↑ Rumburak:
Máš pravdu :-). Já se to vždycky snažím vysvětlit co nejsnadněji, až tam udělám pár nepřeností. :-)
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#13 21. 10. 2014 12:30
- lukasstork

- Příspěvky: 57
- Reputace: 0
Re: Limita výrazu s třetí odmocninou
↑ Rumburak: Ahoj mohl bych se zeptat jak to ma bejt potom dal
Offline
#14 21. 10. 2014 12:42
- misaH
- Příspěvky: 13459
Re: Limita výrazu s třetí odmocninou
↑ lukasstork:
Veď už sa to pýtaš inde - to sa nerobí, nerob duplicity, zbytočne obťažuješ.
Offline
#15 21. 10. 2014 13:06
Re: Limita výrazu s třetí odmocninou
Poznamka, vsetko co je vyssie napisane mozes pouzit.
A aj to ![kopírovat do textarea $\lim_{x\to 0}\frac{\sqrt[3]{1+ax}-1}{x}, a \in R$](/mathtex/bb/bb77e775268d1f5004daa90870274611.gif) ze tento zapis nie je nic ine ako definicia dérivacie funkcie
ze tento zapis nie je nic ine ako definicia dérivacie funkcie ![kopírovat do textarea $x\to \sqrt[3]{1+ax}$](/mathtex/e8/e85824870f3d4c7e5dfba2a53e8d3c65.gif) v bode x=0. Tak vyuzi to.
v bode x=0. Tak vyuzi to.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
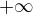 a
a 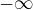
![kopírovat do textarea $\frac{\sqrt[3]{1+ax}-1}{x} = \frac{\sqrt[3]{1+ax}-1}{x} \cdot\frac {(\sqrt[3]{1+ax})^2 + \sqrt[3]{1+ax} + 1}{(\sqrt[3]{1+ax})^2 + \sqrt[3]{1+ax} + 1} = ...$](/mathtex/7b/7bb5f75a06b236ad32d4cc0de4f9a0cc.gif)
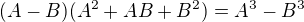 (s
(s 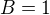 ), pokud nechceme v čitateli
), pokud nechceme v čitateli