Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 05. 05. 2012 19:17
Re: najkrajsia teorema
Pozdravujem
Tak uz je tu majovy problem http://mathcentral.uregina.ca/mp/current/
Celkom zabavny!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#77 17. 05. 2012 13:20
Re: najkrajsia teorema
pozdravujem
Zabavny pekny problem z aritmetiky
Urcite pocet kladnych delitelov csla ktore su mensie ano
ktore su mensie ano  a ktore nie su delitelmy cisla
a ktore nie su delitelmy cisla  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#78 18. 05. 2012 00:36 — Editoval BakyX (18. 05. 2012 00:38)
Re: najkrajsia teorema
1^6 - 2^6 + 3^6 = 666
Offline
#79 20. 05. 2012 14:00
Re: najkrajsia teorema
↑ BakyX:
Ten vysledok je podla mna celkom pekny.
Bravo za tvoje riesenie.
Inac ten vysledok sa da napisat aj takto: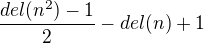
ked 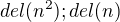 je pocet delitelom cisiel
je pocet delitelom cisiel 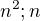
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#80 02. 06. 2012 15:29
Re: najkrajsia teorema
↑ vanok:
tu je riesenie majoveho problemu ( anl. verzia)
http://mathcentral.uregina.ca/mp/previo … y12sol.php
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#81 05. 06. 2012 12:51
Re: najkrajsia teorema
Dva rekreacne problemy od P. Erdös-a
Nech 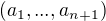 su cele cisla rozdielne medzi sebou v
su cele cisla rozdielne medzi sebou v 
a) Dokazte ze existuju 2 rozne 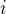 a
a 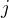 take ze
take ze  a
a 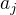 su nesudelitelne.
su nesudelitelne.
b) Dokazte ze existuju 2 rozne 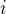 a
a 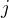 take ze
take ze  deli
deli 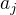 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#82 07. 06. 2012 15:03 — Editoval vanok (07. 06. 2012 15:07)
Re: najkrajsia teorema
Jedno, pekne cvicenie, z teorie grup.
Predpokladajme, ze: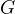 je konecna grupa radu n
je konecna grupa radu n
a 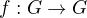 jeden automorfismu grupy
jeden automorfismu grupy  .
.
Polozme 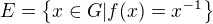
a naviac, ze pocet prvkov mnoziny  je vädci ako n/2.
je vädci ako n/2.
Dokazte ze f je involucia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#83 09. 06. 2012 16:15
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ahoj,
vzhledem k tomu, že f je automorfismus, tak pro  platí:
platí: 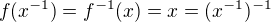 , tj.
, tj. 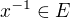 .
.
Označme X jako pogrupu generovanou množinou E. Zřejmě je X=G, protože E má víc než n/2 prvků (a stačí použít Lagrangeovu větu). Tedy každý prvek  lze vyjádřit jako
lze vyjádřit jako 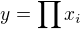 pro
pro  . Z toho, že f je automorfismus a z vlastností prvků E, dostaneme:
. Z toho, že f je automorfismus a z vlastností prvků E, dostaneme: 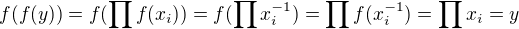 .
.
"Máte úhel beta." "No to nemám."
Offline
#84 09. 06. 2012 16:31
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ahoj. K b): vyjádříme každé číslo  jako
jako 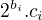 pro
pro  liché a rozdělíme čísla do tříd, kde v každé třídě mají čísla stejnou hodnotu
liché a rozdělíme čísla do tříd, kde v každé třídě mají čísla stejnou hodnotu  . Tříd je n, čísel n+1, takže existují dvě čísla ve stejné třídě - potom tedy jedno z nich dělí druhé.
. Tříd je n, čísel n+1, takže existují dvě čísla ve stejné třídě - potom tedy jedno z nich dělí druhé.
"Máte úhel beta." "No to nemám."
Offline
#85 10. 06. 2012 00:02
Re: najkrajsia teorema
↑ check_drummer:,
Ano to je dokaz pre 
A ako je to ked 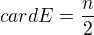 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#86 10. 06. 2012 00:05
Re: najkrajsia teorema
↑ check_drummer:
a) je tiez "jednoduche", vdaka Diriclet, vieme, ze v 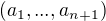 su aspon dve nasledujuce cisla.
su aspon dve nasledujuce cisla.
A tak vdaka Bezout, su nesuleditelne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#87 10. 06. 2012 10:28
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ahoj, řešení a) mě napadlo před chvílí. Stejné jako vidím u tebe.
"Máte úhel beta." "No to nemám."
Offline
#88 11. 06. 2012 13:52 — Editoval OiBobik (11. 06. 2012 16:33)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: najkrajsia teorema
↑ vanok:
Ahoj,
chtěl jsem se zeptat, ty máš řešení pro případ  (přesněji:
(přesněji:  a
a  tvoří podgrupu)?
tvoří podgrupu)?
Já bych řekl, že tam to platit nemusí (tj. že 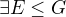 konečné grupy takové, že
konečné grupy takové, že ![kopírovat do textarea $[G:E] =2$](/mathtex/60/60ce4e2f7381b32275d9c2c003b4ba4d.gif) a
a 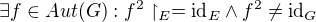 ), ale hledání protipříkladu bude asi dost obtížné.
), ale hledání protipříkladu bude asi dost obtížné.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#89 11. 06. 2012 17:42 — Editoval vanok (11. 06. 2012 22:56)
Re: najkrajsia teorema
↑ OiBobik:
Ahoj, to plati aj pre tu rovnost. .
.
Tu mas jeden dokaz:
uvazujme  podmnozinu grupy
podmnozinu grupy  vytvorenu pevnymy bodmy
vytvorenu pevnymy bodmy 
 je pochopitelne podgrupa grupy
je pochopitelne podgrupa grupy  a to je najvadcia podgrupa na ktorej f je involucia.
a to je najvadcia podgrupa na ktorej f je involucia. obsahuje mnozinu
obsahuje mnozinu  .
.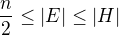
Predpokladajme, ze  , a vtedy
, a vtedy 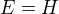 ;a index
;a index  je
je  v grupe
v grupe  .
.
Nech je 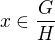 , take, ze
, take, ze  je disjunktne zjednotenie
je disjunktne zjednotenie  a
a 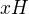
Akoze 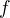 je bijektivna, a
je bijektivna, a  je f-stabilna,
je f-stabilna,
tak 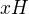 je tiez f-stabilne
je tiez f-stabilne
Pre take  , existuje
, existuje  take ze
take ze 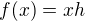 .
.
Ale potom 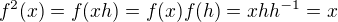
To znamena, ze 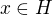 , co je spor.
, co je spor.
Z toho mame  , no vsak
, no vsak 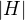 musi delit
musi delit  , tak
, tak 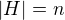
Konkluzia  a
a  je involucia na
je involucia na  .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#91 11. 06. 2012 18:11
Re: najkrajsia teorema
↑ OiBobik:
Mam aj ine, co su tiez "pekne", mam tu take dat z casu na cas?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#92 11. 06. 2012 18:24
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: najkrajsia teorema
↑ vanok:
Pakliže myslíš nějaké takovéto problémky, tak já bych byl určitě pro : ))
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#93 11. 06. 2012 20:26
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ahoj, určitě podobné problémy rádi uvítáme - jen bych se přimlouval za to, aby každý problém měl své vlastní vlákno (téma, příspěvek).
"Máte úhel beta." "No to nemám."
Offline
#94 11. 06. 2012 20:29
Re: najkrajsia teorema
↑ check_drummer:,
Ano, ale tu davam tie najkrajsie ( podla mna )
Inac pochopitelne nebudem vahat otvorit vzdy nove vlakno.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#95 11. 06. 2012 20:48
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ahoj, asi máš v textu drobný překlep: nerovnosti jsou zde opačně:  .
.
"Máte úhel beta." "No to nemám."
Offline
#96 11. 06. 2012 20:54
Re: najkrajsia teorema
↑ check_drummer:
ten predpoklad mi dal spor, tak preto plati opacna nerovnost...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#97 11. 06. 2012 21:06
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ale pokud H obsahuje E, pak je nutně 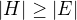 . Rovněž předpokládáme (je to předpoklad celého tvrzení), že
. Rovněž předpokládáme (je to předpoklad celého tvrzení), že  a tedy
a tedy 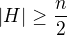 . Jestli jsem
. Jestli jsem
myšlenku důkazu pochopil správně, tak pro spor předpokládáme, že místo obou nerovností je rovnost, tj.  .
.
"Máte úhel beta." "No to nemám."
Offline
#98 11. 06. 2012 21:14
Re: najkrajsia teorema
nie, lebo som ukazal, ze x, ktore je v xH musi patrit do H, a tak |H| = n ( to je ta kontradikcia)
ale predpoklad bol tiez: Bud 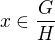 ,
,  je disjunktne zjednotenie
je disjunktne zjednotenie  a
a 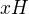
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#99 11. 06. 2012 22:21
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Takže abychom si to shnuli: která z obou nerovností je špatně?
1) 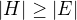
2) 
Děkuji
"Máte úhel beta." "No to nemám."
Offline
#100 11. 06. 2012 23:06 — Editoval vanok (12. 06. 2012 08:56)
Re: najkrajsia teorema
↑ check_drummer:
Obidve su spravne.
1) 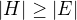 vdaka definici H
vdaka definici H
2)  to je hypoteza.
to je hypoteza.
Inac mal som preklep v mojom preklade do SK (lebo som to nacmaral po FR, a z toho som to prelozil ...ale v preklade uz som nerozmyslal co som mal v originale... lebo matematiku myslim po FR)
Zda sa mi ze to sedi teraz ako treba.
Klucova myslienka, myslim si, je uvazovat tu grupu H.
Tak dobru noc.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
 .
. 
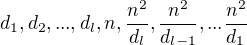
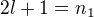 máme
máme  , čo je počet deliteľov
, čo je počet deliteľov 
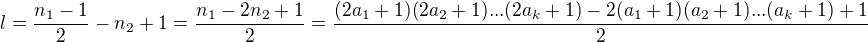
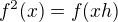 . To je chytré : ))
. To je chytré : ))