Matematické Fórum

Sulfan · 12. 10. 2011 17:05

Ahoj,

mám danou hypotézu, kterou potřebuji dokázat, zní následovně:

$sup\{ \frac{x^8-x^6+x^2-x}{x^8+x^2+2} | x \in \mathbb{R}\}=1$

1. předpoklad pro supremum (horní závora) ve tvaru $\left (\forall x\in\mathbb{R} \right )\left ( \frac{x^8-x^6+x^2-x}{x^8+x^2+2}\leq 1 \right )$ se dokáže snadno, zasekl jsem se však u 2. předpokladu, který zní:

2. $\left (\forall \varepsilon <1 \right )\left ( \exists x\in\mathbb{R} \right )\left ( \frac{x^8-x^6+x^2-x}{x^8+x^2+2}>\varepsilon \right )$

toto tvrzení jsem převedl na tvrzení (za použití dělení polynomů polynomem se zbytkem):

$\left (\forall \varepsilon <0 \right )\left ( \exists x\in\mathbb{R} \right )\left ( \frac{-x^6-x-2}{x^8+x^2+2}>\varepsilon \right )$

z čehož následně:

$\left (\forall \varepsilon >0 \right )\left ( \exists x\in\mathbb{R} \right )\left ( \frac{x^6+x+2}{x^8+x^2+2}<\varepsilon \right )$

A dál jsem se zatím nedostal, hledám tedy nějaký šikovný odhad nebo fintu, jak pokračovat. Samozřejmě by to nějak šlo například limitou, ale ty jsou pro tento příklad zapovězeny.

Děkuji za jakoukoliv radu.

Stýv · 12. 10. 2011 19:28

pro x>2 ten zlomek můžeš shora odhadnout 3x^6/x^8, to se ti pokrátí a kvadratickou nerovnici prostě vyřešíš

Sulfan · 12. 10. 2011 21:03 — Editoval Sulfan (12. 10. 2011 21:06)

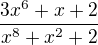↑ Stýv: Pokud je to zamýšleno takhle $\frac{3x^6+x+2}{x^8+x^2+2}$ tak mě nějak nenapadá co pokrátit ..?

Edit: aha chápu, odečtu ze jmenovatele x^2+2 a v čitateli pro x>2 dokážu, že 3x^6+x+2>x^6+x+2 , díky :)

Matematické Fórum

#1 12. 10. 2011 17:05

Supremum množiny

#2 12. 10. 2011 19:28

Re: Supremum množiny

#3 12. 10. 2011 21:03 — Editoval Sulfan (12. 10. 2011 21:06)

Re: Supremum množiny

Zápatí