Matematické Fórum

r2d2 · 18. 10. 2011 14:09

Ahoj, potřeboval bych prosím poradit, pomoct , napovědět, při řešení následující úlohy.
Nalezněte rovnici tečny grafu funkce v bodě 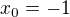$x_0 = -1$ Funkce je $f(x) = 2(arctg(x))^{cos(2\pi x)}$
Funkci jsem derivoval takto:
$f'(x) = e^{cos(2\pi x) \cdot ln(2arctg(x))} \cdot \left( -2\pi sin(2\pi x) \cdot(ln(2arctg(x)) + cos(2\pi x) \cdot \frac {2}{x^2+1} \cdot 1 \right)$
Potom jsem dostal tuto hodnotu pro $f(-1) = -\frac{\pi}{2} \cdot (0 + 1) = -\frac{\pi}{2}$ a pro $f'(-1) = -\frac{\pi}{2}$ a tudíž by rovnice tečny měla být $y + \frac{\pi}{2} = -\frac{\pi}{2}x +\frac{\pi}{2}$ což se rovná $y = -\frac{\pi}{2}x$
Ale jak jsem koukal ve wolframu tak toto pravděpodobně rovnice tečny v bodě x = -1 nebude? Nepodíval by se někdo prosím na to kde je chyba a neřekl jestli je v derivaci a nebo v dosazení bodů? ( Možná obojí )
Děkuji mnohokrát

Jenda358

↑ r2d2:
Ahoj. Pokud je zadání takové jak píšeš, pak se exponent $\cos(2 \pi x)$ vztahuje pouze na $arctg(x)$ , ne na tu dvojku, je to tak?
V tom případě není důvod dávat tu dvojku do argumentu přirozeného logaritmu, jak to máš napsáno tady: $e^{cos(2\pi x) \cdot ln(2arctg(x))}$ .

EDIT: Navíc je třeba mít na pamětí, že derivace $\ln[arctg(x)]$ se rovná $[arctg(x)]^{-1} \frac{1}{x^2+1}$ .

r2d2 · 18. 10. 2011 14:41

↑ Jenda358:no to je vlastně pravda, čili je to $2e^{cos(2\pi x) \cdot ln(arctg(x))} ...$ a tak dále? A je to potom správně zderivováno?

r2d2 · 18. 10. 2011 14:43

↑ Jenda358:ale stejně, to by přeci na výsledku nemělo nic změnit, i když jen náhodou.

Jenda358

↑ r2d2:
Myslím, že máš špatně i derivaci součinu a složené funkce. viz můj EDIT

r2d2 · 18. 10. 2011 14:50 — Editoval r2d2 (18. 10. 2011 14:51)

↑ Jenda358:takže tedy $[ln(arctg(x))]' = \frac{1}{arctg^2(x)+1} \cdot \frac{1}{x^2 + 1} \cdot 1$ . Je to správně?

Jenda358 · 18. 10. 2011 14:53

↑ r2d2:
Ne.
$[ln(arctg(x))]' = \frac{1}{arctg(x)} \cdot \frac{1}{x^2 + 1}$

r2d2 · 18. 10. 2011 14:55

↑ Jenda358: jo jasně to byla chyba v tý rychlosti, to mi dává smysl.

r2d2 · 18. 10. 2011 14:56

↑ Jenda358:Tak já to jdu předělat na papíru a podívám se jestli mi ta tečna vyjde a pak sem přidám to co mi vyšlo, díky za pomoc

r2d2 · 18. 10. 2011 15:21

Takže $f'(x) = 2e^{cos(2\pi x) \cdot ln(arctg(x))} \cdot \left( -2\pi sin(2\pi x) \cdot(ln(arctg(x)) + cos(2\pi x) \cdot \frac{1}{arctg(x)} \cdot \frac {1}{x^2+1} \cdot 1 \right)$
A pro $f(-1) = -\frac{\pi}{2}$ a $f'(-1) = 1$
Takže rovnice by měla být $y = x+1 - \frac{\pi}{2}$ a koukal jsem na to a myslím, že by to tak mělo být správně. Odkaz
(Poznámka na okraj: nevím jak mám wolfram přemluvit aby mi ukazoval dvě funkce vykreslené a ještě k tomu na x-ové pro určitý interval.?)

r2d2 · 18. 10. 2011 15:23

↑ r2d2: Díky moc za pomoc:-)

Jenda358 · 18. 10. 2011 15:28

↑ r2d2:
Není zač, je to dobře.

r2d2 · 18. 10. 2011 15:42 — Editoval r2d2 (18. 10. 2011 15:56)

↑ Jenda358:Můžu mít ještě jednu otázku? Jak bude rovnice normály? Mě vyšlo, že $y = -x -1 -\frac{\pi}{2}$ . Ale když jsem se koukal na graf tak tato přímka funkci neprotne a normála by jí měla kolmo protnou, čili toto asi není správně rovnice normály, ne? Viz odkaz wolfram

Jenda358 · 18. 10. 2011 21:26

↑ r2d2:
Omlouvám se za pozdní reakci. $y = -x -1 -\frac{\pi}{2}$ je správně. Tato přímka původní funkci určitě protne. Možná to tak na WolframAlpha moc nevypadá, ale je to tak.

Matematické Fórum

#1 18. 10. 2011 14:09

Tečna grafu funkce - složitá derivace

#2 18. 10. 2011 14:37 — Editoval Jenda358 (18. 10. 2011 14:46)

Re: Tečna grafu funkce - složitá derivace

#3 18. 10. 2011 14:41

Re: Tečna grafu funkce - složitá derivace

#4 18. 10. 2011 14:43

Re: Tečna grafu funkce - složitá derivace

#5 18. 10. 2011 14:46 — Editoval Jenda358 (18. 10. 2011 14:49)

Re: Tečna grafu funkce - složitá derivace

#6 18. 10. 2011 14:50 — Editoval r2d2 (18. 10. 2011 14:51)

Re: Tečna grafu funkce - složitá derivace

#7 18. 10. 2011 14:53

Re: Tečna grafu funkce - složitá derivace

#8 18. 10. 2011 14:55

Re: Tečna grafu funkce - složitá derivace

#9 18. 10. 2011 14:56

Re: Tečna grafu funkce - složitá derivace

#10 18. 10. 2011 15:21

Re: Tečna grafu funkce - složitá derivace

#11 18. 10. 2011 15:23

Re: Tečna grafu funkce - složitá derivace

#12 18. 10. 2011 15:28

Re: Tečna grafu funkce - složitá derivace

#13 18. 10. 2011 15:42 — Editoval r2d2 (18. 10. 2011 15:56)

Re: Tečna grafu funkce - složitá derivace

#14 18. 10. 2011 21:26

Re: Tečna grafu funkce - složitá derivace

Zápatí