Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 10. 2011 18:52 — Editoval vanok (25. 10. 2011 20:35)
Re: Sequence
Hi ↑ Marian:,
Empirically I observe that:
(Terms pairs of the sequence of Fibonacci)
and
(the Golden Ratio )
Obviously , everything remains to demonstrate in a rigorous way
Remark
Sincerely Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 27. 10. 2011 11:25 — Editoval Rumburak (27. 10. 2011 20:30)
Re: Sequence
Offline
#4 27. 10. 2011 12:29
Re: Sequence
↑ Rumburak:
Small observation: is not just
is not just
Remplaced by
Sincerely Vananok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 27. 10. 2011 13:21
Re: Sequence
↑ Rumburak:
That can arrive at too, like that our solutions agree
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 31. 10. 2011 08:11
Re: Sequence
Here is other interesting solution ...
Offline
#9 01. 11. 2011 15:13
#11 02. 11. 2011 12:38
Re: Sequence
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#12 02. 11. 2011 13:02
Re: Sequence
Offline
#13 02. 11. 2011 13:28
Re: Sequence
↑ Marian:
Just a note - you are right that the reccurence relation  can be solved similarly. If we we set
can be solved similarly. If we we set  and
and  then
then  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline

 in the following way:
in the following way:
 for all positive integers
for all positive integers  .
. ?
?![kopírovat do textarea $F(n)=\frac1{\sqrt5}\[\(\frac{1+\sqrt5}2 \)^n-\(\frac{1-\sqrt5}2\)^n\]$](/mathtex/6e/6e131a1147f761fa79a6d9268af3fa0d.gif)
 satisfy equation
satisfy equation  .
.  ? First we'll find a necessary condition for such hypothese.
? First we'll find a necessary condition for such hypothese.  is a sequence satisfying
is a sequence satisfying ,
,  .
.  ,
,  ,
,  ,
, 
 .
.  , its roots:
, its roots:  , general solution of (2):
, general solution of (2): .
.  .
. 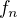 is a positive integer. Positivity from (5), (6) , integrity from (3), (2).
is a positive integer. Positivity from (5), (6) , integrity from (3), (2).  it is quite easy. Therefore
it is quite easy. Therefore ,
,  .
.  .
. we obtain
we obtain


 for
for  is constant and every term of this sequence equals
is constant and every term of this sequence equals 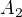 . However, easy computation shows that
. However, easy computation shows that  and in virtue of the previous facts we get that
and in virtue of the previous facts we get that  .
. is an integer sequence. Solving this simple difference equation gives the explicit formula for the general term
is an integer sequence. Solving this simple difference equation gives the explicit formula for the general term 
 and
and  of positive integers in the following way:
of positive integers in the following way: and
and  are coprime for each
are coprime for each 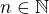 and
and
 are defined by finite continued fractions. It can be proved by induction that
are defined by finite continued fractions. It can be proved by induction that
 is the Fibonacci sequence, i.e.
is the Fibonacci sequence, i.e. 
 and
and  ,
, 


 ,
, 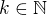 and
and
 is a sequence of positive integers.
is a sequence of positive integers. .
.