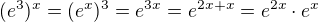Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 06. 2008 16:21
Integral
Zdravím, potreboval bych pomoci s priklady u kterych si nevim rady s postupem.
Jde o neurcite integraly:
1) [2 . (e) na (3x) + 24 . (e) na (x)] / [ (e) na (2x) + 9]
2) arcos (x/3)
Premyslim nad nimi uz dlouho(hlavne nad prvnim), ale porad me nic nenapada at zkousim co zkousim porad nevim. Diky.
Offline
#2 21. 06. 2008 16:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integral
↑ Cipisek:
u prvniho - rozepsat e^(3x) jako e^(2x) * e^(x) a vytknout e^(x) pro cely citatel
Pak substituce e^x = t.
OK?
Offline
#3 21. 06. 2008 17:04
Re: Integral
↑ jelena:
Diky za odpoved. Jenom si ted nejsem uplne jisty kdyz je (e) na (3. x) jestli je to mozna timto zpusovem rozlozit. Podle pravidel pro mocniny tu mam ze podobny tvar se rozklada na [(e) na (3)] na(x). V exponentu by muselo byt 3+x,aby to slo, ale mozna se pletu. Take jsem se snazil vymyslet nejaky spusob pro substituci, ale nevedel jsem jak pokratit promennou kterou nahrazuji:(
Offline
#4 21. 06. 2008 17:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integral
↑ Cipisek:
e^(3x) = e^(2x) * e^(x) = e^(2x+x) =e^(3x) myslim, ze to tak bude
e^(3x) = (e^3)^x nebo (e^x)^3 asi nevyresi problem, jelikoz po substituci e^x = t mame e^xdx =dt
Zkus to dat do nejakoho online vypoctu.
Offline