Matematické Fórum

etchie · 30. 10. 2011 12:43

vseobecne a celkom jasne riesenie sustavy rovnic pomocou matic je:
$\textbf{A}.\textbf{x}=\textbf{B}$
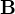kde $\textbf{A}$ je stvorcova matica s koeficientami sustavy rovnic, $\textbf{x}$ je vektor rieseni a $\textbf{B}$ je vektor pravych stran
toto sa riesi upravou: $\textbf{A}^{-1}\textbf{A}.\textbf{x}=\textbf{A}^{-1}\textbf{B}$ a z toho teda vyplyva riesenie $\textbf{x}=\textbf{A}\backslash\textbf{B}$ a vola sa to delenie zlava - az potialto jasne

ked je vsak zadanie uvedene ako: "Rieste sustavu algebraickych rovnic pomocou praveho maticoveho delenia a inverzie"
tak by som mohol na zaklade definovanych maticovych operacii
$\textbf{A}\backslash\textbf{B}=\textbf{A}^{-1}.\textbf{B}$ a
$\textbf{A}/\textbf{B}=\textbf{A}.\textbf{B}^{-1}$

zapisat (dufam), ze $\textbf{x}=\textbf{A}\backslash\textbf{B}=\textbf{A}^{-1}/\textbf{B}^{-1}$ a to by aj zodpovedalo zadaniu pre prave maticove delenie a inverziu.
bohuzial 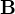$\textbf{B}$ je vektor a teda neviem z neho urobit $\textbf{B}^{-1}$ a teda ani vyriesit tymto sposobom sustavu rovnic

poradite ?

mne osobne z toho vychadza, ze nie je mozne pouzit prave maticove delenie, ale mozno sa mylim

dakujem

vanok · 30. 10. 2011 13:16

Ahoj ↑ etchie:,
Osobne pojem maticoveho delenia nepoznam,
ale preco ho treba dofinovat, ked sa da vyjadrit pomocou inverzivnej matice.
Alebo som nepochopil definiciu co si vysie napisal

Jedina myslienka, ako presjt z lava do prava je tranzpozicia. ( pozor transposovanie vektoru stlpca x je RIADOK)

Napis podrobnejsie o tom zvlastnom deleni; to ma intriguje.

Srdecne Vanok

etchie · 30. 10. 2011 14:24

↑ vanok:

aha, tak uz viem, ze delenie matic zlava a sprava, nie je vseobecny matematicky pojem, ale ze je to zjednoduseny zapis, ktory je definovany v matematickych modelovacich nastrojoch ako Matlab, Octave a spol.
mal som dojem, ze je to vseobecna operacia - ale ako sa ukazalo, tak nie je.

cize aby sme ostali vo vseobecnej matematickej rovine, tak upravim moju otazku takto:
je mozne vypocitat sustavu rovnic zadanu ako $\textbf{A}.\textbf{x}=\textbf{B}$ takym sposobom, ze na pravej strane pouzijem vztah $\textbf{A}.\textbf{B}^{-1}$ + nejake potrebne dalsie upravy ? alebo to mozne jednoducho nie je ?
priklanam sa skor k druhej moznosti, a to z dovodu, ktory som uviedol v prvom prispevku. a text zo zadania povazujem bud za preklep alebo za chytak, v ktorom si student ma uvedomit, ze pomocou praveho delenia to nebude fungovat.

mák · 30. 10. 2011 14:41

Já to řeším takto:
$\textbf{B}.\textbf{A}^{-1}$
a nic víc není potřeba...
(tedy pokud je A čtvercová matice s koeficienty a v B jsou výsledky rovnic)

etchie · 30. 10. 2011 14:54

↑ mák:
nasobenie matic je nekomutativne, takze spravny zapis mus byt $\textbf{A}^{-1}.\textbf{B}$ , ale to je prave to jasne riesenie, ktore urcite funguje

vanok · 30. 10. 2011 16:36

↑ etchie:
dakujem za odpoved

Poznamka o sterilnych metodach:

To vsetko funguje len ak 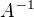$A^{-1}$ existuje
a ak chces na silu pouzit $\textbf{B}^{-1}.\textbf{A}$ tak mame
$$\textbf{A}^{-1}.\textbf{B}$^{-1} =\textbf{B}^{-1}\textbf{A}$ ale navyse
$B^{-1}$ musi existovat.

:-)

etchie · 30. 10. 2011 18:10

↑ vanok:

no ved prave...
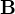$\textbf{B}^{-1}$ nemoze existovat, kedze $\textbf{B}$ je vektor pravych stran sustavy rovnic, teda nie je to stvorcova matica.
zatial co $\textbf{A}^{-1}$ existuje vzdy, pretoze matica $\textbf{A}$ je zarucene stvorcova matica a vzdy k nej musi existovat jej inverzna matica.
to co nam zarucuje, ze $\textbf{A}$ je stvorcova matica je, ze sustava rovnic (aby bola riesitelna) musi pozostavat z tolkych rovnic, kolko je v nej neznamych.
existuju sice aj sustavy rovnic s parametrom, ale tie (myslim si) sa numericky t.j. pomocou matic nedaju riesit tak ci tak

vanok · 30. 10. 2011 18:14 — Editoval vanok (30. 10. 2011 18:16)

↑ etchie:
Ano cize jedina sytucia co je mozna su matice typu (1;1) cize cisla.... a este $B$ musi byt nenulove cize jej jedine clen je nenulovy
a preto som napisal<<<< Poznamka o sterilnych metodach:>>>>

Matematické Fórum

#1 30. 10. 2011 12:43

Riesenie sustavy rovnic pomocou matic

#2 30. 10. 2011 13:16

Re: Riesenie sustavy rovnic pomocou matic

#3 30. 10. 2011 14:24

Re: Riesenie sustavy rovnic pomocou matic

#4 30. 10. 2011 14:41

Re: Riesenie sustavy rovnic pomocou matic

#5 30. 10. 2011 14:54

Re: Riesenie sustavy rovnic pomocou matic

#6 30. 10. 2011 16:36

Re: Riesenie sustavy rovnic pomocou matic

#7 30. 10. 2011 18:10

Re: Riesenie sustavy rovnic pomocou matic

#8 30. 10. 2011 18:14 — Editoval vanok (30. 10. 2011 18:16)

Re: Riesenie sustavy rovnic pomocou matic

Zápatí