Matematické Fórum

kiki · 29. 06. 2008 21:56

Ahoj,

Ráda by jsem Vás poprosila o pomoc, mám zadanou tuto f-ci.

f(x)= arccos(1/1+x^2+y^2)

mám vytvořit graf, vypočítat tot.diferencál, tečnou rovinu a druhé parciální derivace.

Moc děkuju za jakoukoliv pomoc

jelena · 29. 06. 2008 22:12 — Editoval jelena (29. 06. 2008 22:31)

↑ kiki:

Zdravim :-)

Tady najdes hodne podrobne vysvetlene postupy a resene priklady: http://mathonline.fme.vutbr.cz/Matemati … fault.aspx

Zde muzes kontrolovat parcialni derivace: http://old.mendelu.cz/~marik/maw/index. … m=derivace

pro nalezeni definicniho oboru vychazej z toho, ze:
1/(1+x^2+y^2) ma byt v intervalu <-1, 1> a zaroven 1+x^2+y^2 se nesmi rovnat 0

Az narazis na konkretni problem, tak se ozvi tady Hodne zdaru :-)

Editace: k nasledujicimu prispevku kolegy Olina nemam co dodat, je to naprosto spravne doplneni k bezproblemovemu nalezeni definicniho oboru, to moje doporuceni bylo pro zakladni zapis jak se dostat k definicnimu oboru.

Pro jistotu dotaz - v puvodnim zadani chybi zavorka - je to spravne tak, jak jsem umistila, tedy, ze (1+x^2+y^2) je vse v jmenovateli?

Olin · 29. 06. 2008 22:20

Já jen k tomu def. oboru dodávám, že $1+x^2+y^2$ se pro reálná x, y nerovná nule nikdy a taky to bude vždy větší nebo rovno jedné, takže se převrácená hodnota toho výrazu určitě vleze do $(0;\, 1 \rangle$ . Tím pádem je definičním oborem $\mathbb{R}^2$ .

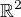Pro tečnou rovinu bude asi zapotřebí znát ten bod, ve kterém se má dotýkat…?

Parciální derivace vypočítáš normálně jako derivace složené funkce.

jelena · 03. 07. 2008 20:43 — Editoval jelena (03. 07. 2008 20:44)

↑ kiki:

kiki napsal(a):
Ahoj ,
už jsem psala a mám zadanou f-ci. f(x,y)=arccos (1/1+x^2+y^2) a m8m vztvo5it graf (tj. půdorys /5 vrstevnic/ a bokorysy /5/ a mám zvolit body P1,P2,P3 a zakreslit je do grafů, tak aby byla patrná jejich souvislost
určit def.obor který je R2 mám zakreslit do rovony xy
A(odm.2/2; -odm.2/2) - tečná rovina a s jeho pomocí odhadnout f-ční.hodnotu v bodě B.
B(1;-1)

Budu pokracovat v tom tematu, kde je "dekuji", ale v tom horku nerucim za uplnou presnost, predem dekuji kolegum za namitky :-)

1. ↑ Olin: uzavrel nalezeni definicniho oboru konstatovanim, ze je to rovina 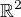$\mathbb{R}^2$ .

2. "pudorys" jsou vrstevnice tvorene rezem rovinou rovnobeznou s rovinou xOy (neboli z=c). Jelikoz vyraz
$1+x^2+y^2$ nabyva pouze kladnych hodnot, obor hodnot funkce z=f(x, y) je v intervalu <0, pi/2)

$arccos(\frac{1}{1+x^2+y^2})=c$

$\frac{1}{1+x^2+y^2}=cos{c}$

pouzijeme takove hodnoty c, aby se "dobre" pocital cos(c), napriklad 0, pi/6, pi/4, pi/3..., ale neni to nutne dodrzet (pi/2 ovsem nedosadime)

napriklad pro pi/3 dostaneme> $\frac{1}{1+x^2+y^2}=cos{\frac{\pi}{3}}$

$\frac{1}{1+x^2+y^2}=\frac{1}{2}$

$x^2+y^2=1$

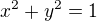
Po dosazeni do zadani funkce a po upravach dostaneme rovnice kruznic - to jsou pudorysne vrstevnice.

3. "bokorys" - jsou rezy tvoreny rezem rovinou rovnobeznou s zOx, tedy y=k.

Za y muzeme dosazovat v podstate cokoliv, napriklad 0 - "centrální rez":

$arccos(\frac{1}{1+x^2+0})=z$

$arccos(\frac{1}{1+x^2+k^2})=z$ coz pro hodnoty k=0 nebo 1 nebo 2 vypada asi takto:

http://forum.matweb.cz/upload/344-kik.jpg

Zaver zadani - jak se hleda tecna rovina a priblizna hodnota (pomoci totalniho diferencialu) je dobre popsano v materialech, na ktere se odkazuji v predchoyim prispevku a jeste tady : http://www.math.muni.cz/~plch/mapm/protisk.pdf

Pokud se nepodari pokracovat, tak se ozvi tady.

Matematické Fórum

#1 29. 06. 2008 21:56

funkce více promněnných

#2 29. 06. 2008 22:12 — Editoval jelena (29. 06. 2008 22:31)

Re: funkce více promněnných

#3 29. 06. 2008 22:20

Re: funkce více promněnných

#4 03. 07. 2008 20:43 — Editoval jelena (03. 07. 2008 20:44)

Re: funkce více promněnných

kiki napsal(a):

Zápatí