Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Levi-Civitův symbol (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 11. 2011 20:43 — Editoval FliegenderZirkus (03. 11. 2011 19:41)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Levi-Civitův symbol
Ahoj, snažím se ukázat, že 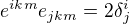 , kde sčítáme přes k,m od jedné do tří. Přepsal jsem to jako
, kde sčítáme přes k,m od jedné do tří. Přepsal jsem to jako 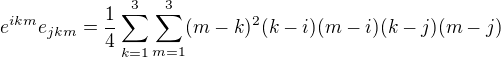
Tady je vidět, že musí platit  , jinak je vždy některá ze závorek rovna nule. Proto:
, jinak je vždy některá ze závorek rovna nule. Proto: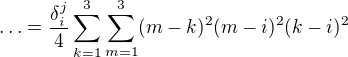 . Teď ale nevím jak dál...
. Teď ale nevím jak dál...
Offline
- (téma jako vyřešené označil(a) FliegenderZirkus)
#2 02. 11. 2011 23:19
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Levi-Civitův symbol
Dá se to snadno ukázat pomocí známého vztahu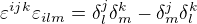
(stačí kontrahovat dva indexy).
Bohužel mě ale nenapadá, jak jednoduše dokázat „známý vztah“.
Offline
#3 03. 11. 2011 11:34 — Editoval FliegenderZirkus (03. 11. 2011 12:05)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Levi-Civitův symbol
↑ Pavel Brožek:
Tenhle vztah jsem chtěl poslat jako druhý dotaz...
EDIT: Srozumitelný důkaz „známého vztahu“ rozepsáním všech možností jsem našel tady: Odkaz
Ten můj postup funguje po rozepsání všech členů, jen je to trochu neohrabané. Kontrakcí 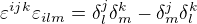 se myslí, že položím např.
se myslí, že položím např. 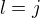 ?
? 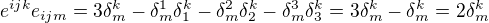
Offline
#4 03. 11. 2011 23:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Levi-Civitův symbol
↑ FliegenderZirkus:
Ten odkazovaný důkaz se mi moc nelíbí, jde vlastně o rozepsání možností. Mám takovou mlhavou vzpomínku, že jsem někdy viděl nějaký hezký důkaz. Možná se později ještě po nějakém podívám.
Kontrakcí (nebo se také říká úžení) dvou indexů i a j se myslí, že jeden index nahradíš tím druhým a vysčítáš přes něj. Provedl jsi to tedy správně.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Levi-Civitův symbol (TOTO TÉMA JE VYŘEŠENÉ)