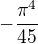Matematické Fórum

thriller · 04. 07. 2008 19:20

Ahoj,
ví někdo, jak na tento integrál $\int_0^{+ \infty} x^2 \ln (1-exp{-x}) dx$ ?

Zkoušel jsem to per partes, ale to nikam nevedlo, asi sem někde udělal chybu (na opravu už mi nezbylo místo :)

Výsledek má být $- \frac{\pi ^4}{45}$

Olin · 04. 07. 2008 21:36

No, mathematica s tím nehla (tedy jako neurčitý integrál tam hodila exotické funkce) Tam bude takový nějaký fígl podobný jako při výpočtu integrálu $\int_0^{\infty}\mathrm{e}^{-x^2}\mathrm{d}x$ .

jelena · 05. 07. 2008 12:41 — Editoval jelena (05. 07. 2008 16:03)

↑ thriller:

Zdravim :-)

Zacatek je urcite v poradku, nepouziva se v tom dal rozklad do nejake rady? Myslim, ze ↑ Olin: ma rozumny zaver (jako obvykle, ostatne :-), ze se to nederivuje v elementarnich funkcich.

Z ktereho okruhu je tento integral, pokud neni tajne?

:-) Proc jsi vlastne nepouzil volnou druhou stranu papiru (ted uz alespon chapu, co znamena "ctvereckovany papir" v ceskem pojeti - to je takovy poznamkovy ctverecek :-)

Editace: ted mam dost duvodu pro dobrou naladu :-)

Mariana vidim online, zdravim srdecne :-) zadani je diky mu vyreseno a to vysvetleni je uzasne :-) :-) :-).
Dalsi radost mam, ze kdyz jsem se vcera pokousela stridat reseni se zehlenim, tak jsem dosla ke stejne uprave s logaritmovanim :-) tady jsem neco podobneho navrhla,dal jsem nevedela. A hrozne moc se bavim, ze moje uprava a uprava kolegy thrillera.... - mam totiz na stole uklizeno a nic jineho, nez obalku a volne strany v casopisu jsem nenasla :-) tak se pobavte :-)

http://uloz.to/550235/int.jpg
http://uloz.to/550241/int2.jpg

A zehleni se tez blizi ke konci (ovsem docasnemu) :-) Zdravim vas :-)

Marian · 05. 07. 2008 14:31 — Editoval Marian (05. 07. 2008 14:32)

↑ thriller:

Ten vysledek, ktery si napsal, je skutecne spravne. Substituci exp(-x)=t se da tento integral prevest na tvar
$\int_{0}^{+\infty}x^2\ln (1-e^{-x})\mathrm{d}x=\int_{0}^{1}\ln ^2t\cdot\ln (1-t)\cdot\frac{\mathrm{d}t}{t}.$

Posledne uvedeny integral se da pak spocitat. Plati totiz identita
$\int_{0}^{1}(\ln t)^{2n}\cdot\ln (1-t)\cdot\frac{\mathrm{d}t}{t}=-\frac{4^n}{(n+1)(2n+1)}\cdot\pi ^{2n+2}\cdot |B_{2n+2}|,\quad n\in\mathbb{N},$

kde B_n oznacuje n-te Bernoulliovo cislo. Dosadime-li n=1, je B_4=-1/30. Tedy vysledek je spravne.

Otazkou (a jiste take vyzvou) je nalezeni odpovedi na to, proc tento vzorec funguje. Budu muset trochu popremyslet, ale slibovat nic nebudu. Hodila by se informace, co zrovna berete, at na to nejdu prilis tezkym aparatem.

Marian · 05. 07. 2008 15:37 — Editoval Marian (05. 07. 2008 18:06)

Tak zde v celku jednoduchy dukaz pro hledany integral.

Po prevedni daneho integralu na integral
$\int_{0}^{1}\ln ^2t\cdot\ln (1-t)\cdot\frac{\mathrm{d}t}{t}$
se uvazi rozvoj funkce f(t), kterou definuji jako

Pak funkce f(t) je spojita (v bode t=0 je spojita zprava - vypoctete si prislusnou limitu pro overeni) na intervalu I:=[0,1]. Rozvoj funkce f(t) je
$f(t)=-1-\sum_{k=1}^{\infty}\frac{t^{k}}{k+1}.$

Da se overit, ze pro vsechny body t intervalu I (v pripade krajniho bodu t=0 beru limitu zprava) plati
$\ln ^2t\cdot\left (1+\sum_{k=1}^{\infty}\frac{t^k}{k+1}\right )=\ln ^2t+\sum_{k=1}^{\infty}\ln ^2t\cdot\frac{t^k}{k+1}.$

Oznacime-li dale
$f_k(t):=\ln ^2t\cdot\frac{t^k}{k+1},\qquad k\in\mathbb{N},\:\forall t\in I,$

je videt, ze plati
$\lim_{k\to +\infty}\sup_{t\in I}\left |f_k(t)\right | =0.$

To implikuje, ze
$\int_{0}^{1}\ln ^2t\cdot\ln (1-t)\cdot\frac{\mathrm{d}t}{t}=-\int_{0}^{1}\ln ^2t\left (1+\sum_{k=1}^{\infty}\frac{t^k}{k+1}\right )\,\mathrm{d}t=\nl -\int_{0}^{1}\left (\ln ^2t+\sum_{k=1}^{\infty}\ln ^2t\cdot\frac{t^k}{k+1}\right )\,\mathrm{d}t=\nl -\int_{0}^{1}\ln ^2t\,\mathrm{d}t-\sum_{k=1}^{\infty}\frac{1}{k+1}\cdot\int_{0}^{1}t^k\cdot\ln ^2t\,\mathrm{d}t.$

Dale se primym vypoctem dokaze (neni to tak tezke - nekolik limit), ze pro kazde nezaporne cele cislo k plati identita
$\int_{0}^{1}t^k\cdot\ln ^2t\,\mathrm{d}t=\frac{2}{(k+1)^3}.$

Odtud snadno
$\int_{0}^{1}\ln ^2t\cdot\ln (1-t)\cdot\frac{\mathrm{d}t}{t}=-2\sum_{k=0}^{\infty}\frac{1}{(k+1)^4}=-2\zeta (4)=-2\cdot\frac{\pi ^4}{90}=-\frac{\pi ^4}{45}.$

Proto

$\boxed{\int_{0}^{+\infty}x^2\cdot\ln (1-e^{-x})\,\mathrm{d}x=-\frac{\pi ^4}{45}.}$

EDIT: Uz jsem to poopravil, abych vas netrapil nekorektnimi vyrazy typu 0^0. Pokud uvidite neco nesrozumitelneho nebo nejakou chybu, klidne napiste, vyjasnime to.

Pokud mate jednodussi napad k reseni uvedeneho integralu (nebo integralu obecnejsich - viz muj pripsevek vyse), rad se priucim.

Marian · 05. 07. 2008 16:40

↑ jelena:
Zdravim take, jeleno!

Integraly tohoto typu se resi nekdy prevodem na nekonecnou konvergentni radu. Toto byl tento pripad.

Jsem rad, ze mas uklizeno. Tedy alespon nekdo ma jiz uklizeno. Ja uz uklizim zhruba rok a jeste se mi to nepodarilo poradne dokoncit (nejak to diverguje, prevedu-li to na rec nekonecnych ciselnych rad). Takze kdyz jsem tady jednou daval fotografii se svym pracovnim stolem, tak to stale trva, spise pozoruji zhorseni.

Olin · 05. 07. 2008 17:37

Já bych se jen zeptal, proč považuješ za nějak obtížný ("Dás se ověřit") krok
$\ln ^2t\cdot\left (1+\sum_{k=1}^{\infty}\frac{t^k}{k+1}\right )=\ln ^2t+\sum_{k=1}^{\infty}\ln ^2t\cdot\frac{t^k}{k+1}.$
když je to akorát roznásobení…

Marian · 05. 07. 2008 18:01 — Editoval Marian (05. 07. 2008 18:14)

↑ Olin:

Pro t=0 roznasobovat nelze, protoze pro t jdouci k nule zprava budes mit za sumacnim znakem neurcity vyraz (+oo)*0+. Pro zbyle body intervalu I=[0,1] problem jiste neni.

Jeste presneji takto; musi se overit platnost rovnosti
$\ln ^2t\sum_{k=1}^{\infty}\frac{t^k}{k+1}{=}\limits^{?}\sum_{k=1}^{\infty}\ln ^2t\cdot\frac{t^k}{k+1}, \quad\forall t\in I:=[0,1].$

To je ekvivalentni s overenim faktu, ze
$\lim_{t\to 0^+}\left (1+\frac{\ln (1-t)}{t}\right )\cdot\ln ^2t=0.$

jelena · 05. 07. 2008 18:29

↑ Marian:

Smim take dotaz - sice to logaritmovani jsem take zkousela, ale vice "zvykle" (alespon z toho, co jsem kdy videla a pouzila) mi pripadala moznost rozkladu e^x v radu (po prvnim per partes).
Ale nevedela jsem, jak se zohledni, ze tam je jeste x^3, prislo mi, ze se to nejak divne "rozleza" - to je slovnik, ze :-).

Zejmena kdyz ctu tvoje prospevky, tak vzdy zacnu vahat, ktery krok se pouziva "automaticky" a ktery se musi jeste dokazovat :-(

Ale pokud nejak nemas cas, budu rada i za odpoved "nekdy jindy", dekuji velice :-)

"Uklizeno" je okamzity nestabilni stav, ktery skokove prechazi do stavu stabilniho "neuklizeno" :-)

Marian · 05. 07. 2008 18:52 — Editoval Marian (05. 07. 2008 18:53)

jelena napsal(a):
"Uklizeno" je okamzity nestabilni stav, ktery skokove prechazi do stavu stabilniho "neuklizeno" :-)

Skutecne "pravda", tedy alepson u me. Sama jsi to vymyslela, nebo jej od nekud mas (to at te pripadne mohu citovat). Tak by me zajimal graf a hlavne predpis nejake funkce, ktera ma hodnoty bud nula nebo jedna, procemz nulu (tedy "neporadek") skoro vsude. Treba
$N(x):=[\sin ^2(\sqrt{x})],$
kde [q] znaci celou cast realneho cisla q.

A ten tvuj dotaz k rozvoji exp(x). Kdyz jsem videl vysledek ve tvaru -Pi^4/45, pak jsem tusil, ze to bude smerovat na scitani nekonecne rady typu Riemannova zeta. Jenze pri rozvoji exp(x) do potencni rady by se mi tam vyskytly faktorialy a to bych se patrne tak lehce k tomu vysledku nemusel dostat. Nevim, nezkousel jsem to - ale takhle to citim. Navic nepracuji nejradeji s nevlastnimi mezemi u integralu. Tedy ta transformace puvodniho integralu na integral obsahujici prirozene logaritmy, pricemz meze integralu jsou realna cisla 0 a 1, mi pripadala vyhodna.

jelena · 05. 07. 2008 19:39 — Editoval jelena (07. 07. 2008 23:01)

↑ Marian:

dekuji za doplneni a vysvetleni :-) treba budu mit cas se to jeste podivat ze strany e^x.

Tvrzeni, co uvadim, je original, dlouholetou praxi overeny a hodnym okolim tolerovany. Puvodce tvrzeni a neporadku je stejny - ja :-)

Graf - mozna i nejaka Fourierova rada. Ostatne, cim je vetsi chaos, tim je hezci graf (take moje) - koho by zajimala konstantni primka :-). Konec OT

Editace :-) hledala jsem neco jineho - a co jsem nasla? rozklad pomoci e^(-x) - tedy presne te casti, kterou ma kolega thriller ve stredni casti ctverecku napravo - materialem se sice musite probrat - je to temer v zaveru textu pod vzorcem 1.40, Задача 1.3

http://lgrflab.ru/physbook/tom5/ch1/tex … 2_text.htm

ted mi zbyva si vybavit, co jsem to vlastne hledala :-)

Matematické Fórum

#1 04. 07. 2008 19:20

integrál

#2 04. 07. 2008 21:36

Re: integrál

#3 05. 07. 2008 12:41 — Editoval jelena (05. 07. 2008 16:03)

Re: integrál

#4 05. 07. 2008 14:31 — Editoval Marian (05. 07. 2008 14:32)

Re: integrál

#5 05. 07. 2008 15:37 — Editoval Marian (05. 07. 2008 18:06)

Re: integrál

#6 05. 07. 2008 16:40

Re: integrál

#7 05. 07. 2008 17:37

Re: integrál

#8 05. 07. 2008 18:01 — Editoval Marian (05. 07. 2008 18:14)

Re: integrál

#9 05. 07. 2008 18:29

Re: integrál

#10 05. 07. 2008 18:52 — Editoval Marian (05. 07. 2008 18:53)

Re: integrál

jelena napsal(a):

#11 05. 07. 2008 19:39 — Editoval jelena (07. 07. 2008 23:01)

Re: integrál

Zápatí