Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 07. 2008 12:36 — Editoval matoxy (14. 07. 2008 13:37)
Limity
Zdravím, ako treba rieši? takýto typ limity: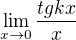 . Prišiel som len k úprave:
. Prišiel som len k úprave: 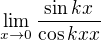 , ale ďalej si s tým k-čkom neviem rady.
, ale ďalej si s tým k-čkom neviem rady.
Výsledok má by? k.
Editácia: Ešte ma napadlo, že sa to dá rozšíri?  , ale potom tam stejne ostane: k cos kx
, ale potom tam stejne ostane: k cos kx
A ešte: 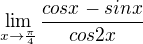 toto vôbec neviem a má výs?
toto vôbec neviem a má výs? 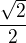 .
.
Tá goniometria mi ide akosi menej než som si myslel.
You know who
(or maybe not)
Offline
#2 14. 07. 2008 13:12 — Editoval jelena (14. 07. 2008 19:47)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Zdravim :-)
je cervenec, odpocivat se ma :-)
K je konstanta predpokladam - nevidim zadny duvod ji "poslat za" sin nebo za cos. 
v teto uprave mas schovan "замечательный предел - přeloženo "pozoruhodnou limitu" - nevim, zda je prihodny slovensky nazev :-)  ,
,
cos0=1. proto ve vysledku je k
OK ?
Offline
#5 14. 07. 2008 13:49
Re: Limity
Tiež som počul, od niekoho, že sa má v júli oddychova?, ale bol som minulý týždeň na takom astronomickom sústredení, tak som si oddýchol... a nabral novú inšpiráciu, a povedal si, že sa pustím do matematickej analýzy, hádam tentokrát úspešnejšie. Začal som limitami.
Ale ten prvý príklad mi aj tak vychádza akosi inak: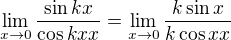 tu vyškrtám k-áčka aj sin x / x a dostanem
tu vyškrtám k-áčka aj sin x / x a dostanem 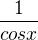 a z toho k mi akosi nejako nevvychádza??
a z toho k mi akosi nejako nevvychádza??
Ten druhý, to je teda jasné, len si ešte zopakujem tie vzorce pre goniometrické funkcie.
You know who
(or maybe not)
Offline
#7 14. 07. 2008 14:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
? muzes na jeden obrazek nakreslit grafy:
y=sin(2x), y=2sinx a pak podiskutujeme :-)
Tu upravu - "vytahnout k" pred sin opravdu nemuzes pouzit. Nejdriv pouzivas rozpis tg(kx) =(sin(kx))/(cos(kx)) a pak pouze donasobis citatel a jmenovatel k. OK?
Offline
#8 14. 07. 2008 22:13 — Editoval matoxy (14. 07. 2008 22:15)
Re: Limity
Noo... keď si uvedomím ako by vyzerali tie grafy tak mi došlo, že to tak nebude a úprava teda bude: 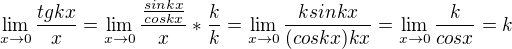 . :)
. :)
Došiel som k tomu tvrdeniu so sínusmi v dôsledku nedorozumenia s tým mojím chybným zadaním a som nad tým či to tak môže by? poriadne neporozmýšľal.
+ Ďakujem za pomoc, ale myslím, že sa ešte v najbližšej budúcnosti ohľadom niečoho podobného ozvem O:-).
You know who
(or maybe not)
Offline
#9 14. 07. 2008 22:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
V juli a v auguste :-) no ked si myslis :-)
Jake bylo soustredeni? a na co bylo zamerene - ostatne uvidime castecne zetmeni Slnka nebo nas to mine?
Zdravim :-)
Offline
#10 15. 07. 2008 10:45
Re: Limity
Sústredenie nebolo myslím zamerané na nič konkrétne. Ale prednášky sme tam mali dos? o astrofotografií, o slnečných hodinách, globálnom otepľovaní (vraj nie je až tak isté, že ho spôsobujú ľudia :))... O tom zatmení nám tuším ktosi vravel, že z Čiech bude pozorovateľné čiastočne, tuším v Hvezdárni vo Valašskom Medziřičí nám to hovorili, tam sme boli na exkurzií a ešte v múzeu TATRA - pekné autíčka len často z nich treba utiera? prach :).
You know who
(or maybe not)
Offline
#11 15. 07. 2008 19:35 — Editoval matoxy (15. 07. 2008 20:26)
Re: Limity
Nakoniec to ani tak dlho netrvalo, čo som sa tu ukázal, s nádejov, že mi niekto pomôže:) Mám takýto príklad : ![kopírovat do textarea $\lim_{x \to 1}\frac{\sqrt[3]{3}-1}{\sqrt x -x}$](/mathtex/3d/3d18f5f9387f4b56b11cc0390af25d23.gif) .
.
Príklady čerpám z tejto stránky: http://www.mojeskola.cz/Vyuka/Php/ , ktorú mi pred časom odporučila jelena. Je to jeden z príkladov ktorý tam má tzv. krokovú kontrolu, avšak je prístupná len po registrácií a to neveim ako sa robí. Sú tam však 4 možnosti čo najskôr spravi?: a.) rozšíri? zlomok ![kopírovat do textarea $\sqrt[3]{3}-1$](/mathtex/86/867dc0fc2b41504c354657c1bf3a2fd3.gif)
b.) rozšíri? zlomok 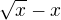
c.) umocníme zlomok na druhou
d.) zavedeme pomocnou neznámou
Skúšal som rozšíri?  , avšak nič rozumné mi nevyšlo, lebo v menovateli bolo stejne x -x, rozšíri?
, avšak nič rozumné mi nevyšlo, lebo v menovateli bolo stejne x -x, rozšíri? ![kopírovat do textarea $\sqrt[3]{3}-1$](/mathtex/86/867dc0fc2b41504c354657c1bf3a2fd3.gif) mi nedáva zmysel, lebo tretioa odmocnina na druhú je nič užitočné. Umocni? na druhú, v tom tiež nevidím zmysel. Zostáva teda len zavedeme pomocnou neznámou, čo si myslím, je inými slovami substitúcia, avšak tá ma nejak rozumne nenapadá.
mi nedáva zmysel, lebo tretioa odmocnina na druhú je nič užitočné. Umocni? na druhú, v tom tiež nevidím zmysel. Zostáva teda len zavedeme pomocnou neznámou, čo si myslím, je inými slovami substitúcia, avšak tá ma nejak rozumne nenapadá.
Vopred ďakujem za pomoc.
EDITACE: už som prišiel na to ako sa tam registrova?, aj na výsledok som nejak prišiel, je to 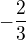 :)
:)
You know who
(or maybe not)
Offline
#12 15. 07. 2008 20:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Zdravim :-)
Ted nejsem si jista, zda resis zadani 7 "z kroku" nebo 37 (pod kapitolou), ale princip je stejny :-)
Muj postup je pro 37.![kopírovat do textarea $\lim_{x \to 1}\frac{\sqrt[3]{x}-1}{\sqrt x -1}$](/mathtex/df/df17c3b34c95f7c4a8c1a8a5b7fa2171.gif)
Uprava - citatel rosirit na vyraz (a^3 - b^3), jmenovatel na vyraz (a^2 - b^2)![kopírovat do textarea $\frac{(\sqrt[3]{x}-1)(\sqrt[3]{x^2}+\sqrt[3]{x}+1)(\sqrt x +1)}{(\sqrt x -1)(\sqrt x +1)(\sqrt[3]{x^2}+\sqrt[3]{x}+1)}=\frac{(x-1)(\sqrt x +1)}{(x -1)(\sqrt[3]{x^2}+\sqrt[3]{x}+1)}=\frac{(\sqrt x +1)}{(\sqrt[3]{x^2}+\sqrt[3]{x}+1)}$](/mathtex/4e/4eccb523f320756a599705e5247189b4.gif)
ted se vrat do limit a dosazuj 1.
Stejny postup by mel byt i u 7.
OK?
Offline
#13 15. 07. 2008 20:36 — Editoval matoxy (16. 07. 2008 00:01)
Re: Limity
Malo to by? pre to sedem som to zas zle napísal, posnažím sa pre budúcnos? by? dôslednejší, no teraz idem hra? s tunajšou pospolitos?ou Investor:). + v tej sedmičke som ešte zaviedol substitúciu a vyriešil to takto: ![kopírovat do textarea $\lim_{x \to 1}\frac{\sqrt[3]{x}-1}{\sqrt x -x}$](/mathtex/0e/0e5e903dd12069b5482a876484735b8e.gif) tu zavedieme
tu zavedieme  a ďalej upravujeme na:
a ďalej upravujeme na:  , čo sa po dosadení rovná
, čo sa po dosadení rovná 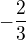
You know who
(or maybe not)
Offline
#14 15. 07. 2008 22:58 — Editoval jelena (15. 07. 2008 23:24)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
I to je mozne :-)![kopírovat do textarea $\sqrt[3]{3}$](/mathtex/81/812a15cf10c23e809036e954d2521e80.gif) sice v zadani neni, zrejme preklep.
sice v zadani neni, zrejme preklep.
-------------
Astronomicke zajimavosti :-)
1. v Opave mame Slunecni soustavu:-)
2. cestovky v Rusku ted poradaji zajezdy smerem na Sibir za ucelem pozorovani zatmeni - vybaveni a pozorovaci plosina je soucasti sluzeb
Offline
#15 16. 07. 2008 00:25
Re: Limity
Správne preklep, ďakujem za upozornenie, no naš?astie sme sa pochopili.
No taký zájazd do Ruska musí teda riadne stá? na také pozorovanie, veď len tá cesta tam a dotrepa? tam pozorovaciu techniku. Ale niekto na zraze vravel o tom, že tam pôjde ak ma pamä? neklame.
K tej Slnečnej sústave, je to zaujímavá vec, len sa mi nepozdáva, že tam píšu, že je to v nejakej mierke. Ak je Zem niekoľko metrov od Slnka a Pluto 9,5 km, to j epribližne 100x-1000x viac pričom ZEM- ŚLNKO = 1AU; PLUTO-SLNKO = cca 40 AU. Avšak priemery tých planét, ktoré sú tam uvedené približne sedia aj s mierkou. Ale keď najbližšie prídem do Opavy tak tie planéty pochodím, ak by som náhodou mal času to, mohla by to by? sranda:).
(Ste mi pripomenula stránku IAN.cz. Sa mi pred časom nedala prida? do hornej lišty, kde mám ostatné často navštevonané, tak som na ňu nejak zabudol.)
You know who
(or maybe not)
Offline
#16 17. 07. 2008 18:26
Re: Limity
Mohly by ste mi pomôc? ešte s týmito príkladmi?
a.) 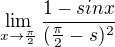 , vôbec neviem čo s tým, je to príklad č. 103
, vôbec neviem čo s tým, je to príklad č. 103
b.)  , rozšíril som zlomok výrazom
, rozšíril som zlomok výrazom  , ale nič rozumné mi z toho nevyšlo. Po úprave som dostal
, ale nič rozumné mi z toho nevyšlo. Po úprave som dostal  . ďalej vôbec neviem čo
. ďalej vôbec neviem čo
You know who
(or maybe not)
Offline
#17 18. 07. 2008 14:49
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Zdravim :-)
K prikladu a) - tam by se velmi dobre hodilo l´Hospitalovo pravidlo a bylo by to rychle. Ale pokud je pozadovana uprava, tak opet se snazim najit pozoruhodnou limitu. nejdriv rozsirim vyrazem (1+sin x).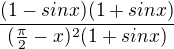
dal budu pouzivat vzorec sin^2 x + cos^2 x=1 a souctove goniometricke vzorce, a sice cos(x) = sin (pi/2 - x)
Pokud se to nepodari, tak se ozvi. OK?
Offline
#19 19. 07. 2008 15:38 — Editoval matoxy (20. 07. 2008 14:04)
Re: Limity
Tiež zdravým:) 
To 2pi v tretom výraze od zadu má by? pi/2, len tex je tvrdohlavý a neviem prečo mi to tam nechce da? tak ako má by?. No výsledok 1/2 uvádzajú aj na stránke. Som si hlavne neuvedomil ten vz?ah, že cos x = sin (pi/2-x). Čo sa týka toho L´Hospitalovho pravidla, tak k tomu som ešte neprišiel.
b.) 
Nejako sa mi zdalo nie dobre rozšírova? dvoma zlomkami.
Ďakujem
Ešte by som rád vedie? ako upravi?, resp. rozloži? takýto výraz: 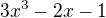 . Je to z príkladu:
. Je to z príkladu: 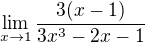 . Skúšal som to rozloži? na nejaký výraz ktorý by obsahoval buď 3x-3, alebo x-1, aby sa to dalo vyškrta?, obidvoje však neúspešne. Nikdy sa mi nepodarilo dosta? tam x^3 bez toho aby som mal x^2.
. Skúšal som to rozloži? na nejaký výraz ktorý by obsahoval buď 3x-3, alebo x-1, aby sa to dalo vyškrta?, obidvoje však neúspešne. Nikdy sa mi nepodarilo dosta? tam x^3 bez toho aby som mal x^2.
You know who
(or maybe not)
Offline
#20 20. 07. 2008 00:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
vse OK, jen jsem trochu upravila zapis, aby bylo pi/2. Take pomoci \\ jsem rozdelila radky. Ale to jsou kosmeticke upravy :-)
Rozklad polynomu 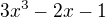 na soucin bude trochu slozitejsi, ale daji se tam pouzit ruzne vychytavky, treba
na soucin bude trochu slozitejsi, ale daji se tam pouzit ruzne vychytavky, treba
a) 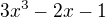 rozepisi 3x^3 jako 2x^3 + x^3 a dal budu vytykat po dvojicich:
rozepisi 3x^3 jako 2x^3 + x^3 a dal budu vytykat po dvojicich:
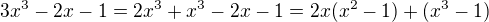 dal, myslim, jasno, ze?
dal, myslim, jasno, ze?
nebo pokud uz vidim, ze vyhledove bude potreba kratit s (x-1), tak se pokusm podelit mnohoclen mnohoclenem 
no a odsud je jiz blizko sem- koreny polynomu a k debate o resitelnosti kubickych rovnic, pripadne k rozkladu polynomu pomoci Hornerova schematu - podrobne tady: http://forum.matweb.cz/viewtopic.php?id=496
Metoda bude zalozena na tom, ze jeden koren rovnice  se pokusime uhodnout - byva obvykle pekny (1. -1. 2. -2 ) - v nasem pripade 1. Ted opet vyuzijeme deleni mnohoclenu mnohoclenem.
se pokusime uhodnout - byva obvykle pekny (1. -1. 2. -2 ) - v nasem pripade 1. Ted opet vyuzijeme deleni mnohoclenu mnohoclenem.
OK?
------------------------------------------------
Slunecni soustava v Opave je trochu zkreslena - vychazeji z toho, ze na namesti ve fontane lezela Zemekoule - tak z ni udelali Slunko. Planety jsou v turisticky zajimavych mistech, ale vzdalenost muze byt zkreslena. Ale pry ne moc :-)
Myslim, ze nejhur dopadl prave Pluto (no, ten celkove nedopadl nic moc, ale mu to nejak nevadi, doufam :-)
Opava je vubec astronomicke mesto - na mistni Slezske univerzite se da studovat obor Astrofyzika :-)
V Opave budes vzdy srdecne vitan, urcite dej vedet, az budes mit v planu se vypravit :-)
Offline
#21 20. 07. 2008 14:27
Re: Limity
To pi/2 som už opravil, nevedel som, že argument sin musí by? v kučeravých zátvorkch keď je zložitejší.
Osviežil som si teda to delenie polynómov a vydelil to: 
Aplikáciou na ten príklad dostaneme: 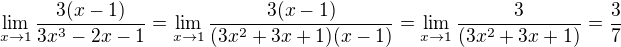 Čo je výsledok, ktorý ponúkajú aj na stránke:)
Čo je výsledok, ktorý ponúkajú aj na stránke:)
You know who
(or maybe not)
Offline
#22 20. 07. 2008 21:36 — Editoval matoxy (21. 07. 2008 16:11)
Re: Limity
Ešte by som potreboval pomôc? s dvomi typmi príkladov:
Pr.105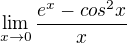 a
a
Pr.126.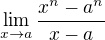 .
.
Potom sa už hádam odhodlám na nevlasné limity a derivácie.
EDITACE: K tomu príkladu 105. som našiel v ďalšej lekcii  a ak platí tento vz?ah, tak ho uplatníme na náš úríklad a dostávame:
a ak platí tento vz?ah, tak ho uplatníme na náš úríklad a dostávame:  Čo je výsledok, ktorý ponúkajú aj na stránke. Len je mi trochu čudné, že ten vzorec dali až v ďalšej lekcii.
Čo je výsledok, ktorý ponúkajú aj na stránke. Len je mi trochu čudné, že ten vzorec dali až v ďalšej lekcii.
+ ja som rád, že je niekto kto mi pomôže s matikou dokonca aj cez prázdniny, takže do večera aj do ďalšieho kľudne počkám. Veď do konca prázdnin ešte času:)
You know who
(or maybe not)
Offline
#23 21. 07. 2008 23:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Zdravim :-)
K 1. prikladu nemam co dodat - take bych to tak resila. V napovede doporucuji pouzit vetu o trech limitach - ale nejak jsem nevymyslela nic prevratneho - stale se to smerovalo k l´Hospitalovi, ktereho zatim mame zakazaneho :-) .
Treba se na to podiva nekdo z kolegu, jak by se to dalo vyuzit.
V 2. priklade se pouzije vzorec 2.5 - je to rozklad na soucin (nebo take muzes zkusit nekolik kroku deleni citatele a jmenovatele. Prvni zavorka (x-a) v citateli se vykrati s jmenovatelem.
Dal uz, myslim, jasne? - uz jen dosadit a za x, dostaneme n(a)^(n-1)
Obe limity se daji moc dobre najit pomoci l´Hospitala, tak se k nim vrat, az to bude procviceno :-)
Offline
#25 22. 07. 2008 17:59
Re: Limity
A ešte by som rád poradi? s takýmito nevlastnými limitami:
63. Vraj treba použi? ten vz?ah, ktorý sme použili aj vyššie u príkladu 105.
Vraj treba použi? ten vz?ah, ktorý sme použili aj vyššie u príkladu 105.
65. 
70.  Ja by som upravoval:
Ja by som upravoval:  Výsledok však uvádzajú 1
Výsledok však uvádzajú 1
86.  Uvádzajú výsledok 0, ale podla mňa je to nekonečno, lebo 1/x ak x->0 je oo a hocičo na nekonečnú, čo je väčšie od 1 je nekonečno nie?
Uvádzajú výsledok 0, ale podla mňa je to nekonečno, lebo 1/x ak x->0 je oo a hocičo na nekonečnú, čo je väčšie od 1 je nekonečno nie?
You know who
(or maybe not)
Offline
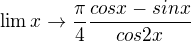 pouzijes vzorec pro cos dvojnasobneho uhlu
pouzijes vzorec pro cos dvojnasobneho uhlu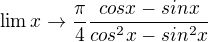 - pouzijes vzorec (a^2 -b^2)
- pouzijes vzorec (a^2 -b^2)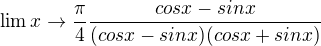 pokratis, dosadis pi/4, a usmernis vysledek.
pokratis, dosadis pi/4, a usmernis vysledek.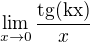 bud jsem to spatne videla nebo byl edit :-)
bud jsem to spatne videla nebo byl edit :-)

 ?
?
 .
.