Matematické Fórum

jelena · 28. 07. 2008 21:06 — Editoval jelena (28. 07. 2008 22:32)

Zdravim :-)

1) Předně bych chtěla uklidnit kolegu matoxy, aby si vůběc nedělal těžkou hlavu z našich nápadů a debat.
Máme stale jul, dokonce počasi se umoudřilo (až moc, dle mého :-) proto je takový prostor na spoustu aktivit :-)

2) Kniha od Mariana je čitelna po vyarchivování pomocí (nebo z) winrar - pokud ho nemás, dá se stahnout (já už mám úspěšně uloženo a "prolistováno", děkuji, Mariane, ale není nad knihu :-)

3) Co jsem to měla zdůvodnit?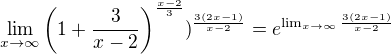

$\lim_{x \to \infty}\left(1+\frac{3}{x-2}\right)^{\frac{x-2}{3}})^{\frac{3(2x-1)}{x-2}}=e^{\lim_{x \to \infty}\frac{3(2x-1)}{x-2}}$ - zda je to regulérní?

používám zde v podstatě stejné zdůvodnění, jak uvádiš v příspěvku ↑↑ BrozekP: - příspěvek 44 - bohužel, odkaz mám pouze na ruskou učebnici, podle které jsem se také učila: http://eqworld.ipmnet.ru/ru/library/boo … 962ru.djvu - str. 174 "stránkování" a 165 originálu.

Jako vnější funkci chapu e^u, vnitřní $u={{\frac{3(2x-1)}{x-2}}\ln ((1+\frac{3}{x-2})^{\frac{x-2}{3}})}$ no a jelikož to vypadá hrůzostrašně, tak používám svoje polopatické pomůcky o točení mocnin :-)

4) Použití 3 limit už neřeším - asi to nebyla vhodná napověda pro 1. kapitolu.

5) Já opravdu chapu jak použití binomické věty, tak i zařazení pod jednu mocninu a ze včeho nejlépe dělení nejvyšší mocninou, což prakticky používám :-) Proč zrovna bin. věta byla zvolena do nápověty - ?? pro autora zadání. Právý důvod nevím :-)

Není nad to dělat několík věci najednou - všechno pák trvá :-)

Navrhuji ukončit naši děbatu a řešit pouze otázky kolegy matoxy. Děkuji moc za dosavadní pomoc :-)

matoxy · 28. 07. 2008 21:35

Jelena stiahol som si WinRAR a úspešne rozbalil tú knihu, tak sa na ňu pozriem, ale myslím, že ešte budem pokračova? aj zo stránky mojeskola, celkom som si na ňu už totiž zvykol:).

jelena · 28. 07. 2008 21:48

↑ matoxy:

Určitě pokračuj - třeba se ještě něco pěkného prodebatuje - snad se na nás nezlibiš, že v tématu máš trochu zmatek (ne tvoji vinou, samozřejmě :-)

matoxy · 28. 07. 2008 21:55

Určite sa nezlobím. Táto téma sa mi náhodou páči. Keď som si ju prelistoval tak spätne, všimol som si, že je v nej taká postupnos? či systém:).

Pavel Brožek

↑ jelena:

Souhlasím s ukončením této debaty, takže už do příspěvku nedám žádný otazník, abys nemusela reagovat :-)

3) Myslel jsem to v tomto smyslu - pokud by někdo tuto úpravu dělal při výpočtu do fyziky nebo jinam (tim mam na mysli, že předmětem zájmu nejsou způsoby řešení limit), tak mi to nevadí. Tady ale jde o to, že matoxy nebo někdo jiný, kdo si to bude studovat, tenhle postup třeba nezná. Když uděláš tenhle krok, tak v lepším případě si ten člověk dokáže, že je to správně, nebo se zeptá na podrobnosti té úpravy. Ale v nejhorším případě to ten člověk pochopí tak, že smí vyčíslit nějakou část limity a pokračovat dál. Přijme to jako novou úpravu co smí dělat. Tak tomu bych chtěl předejít. Tak až budeš tuhle úpravu zase používat, tak třeba napiš, že to neni samozřejmá úprava a ať se dotyčný ozve, pokud mu není jasná.

Edit: Po letech jsem se dostal k tomuto svému příspěvku a koukám, že se nějak časem pokazila diakritika a tím se ve slově ať objevil otazník. Tím má první věta ztratila na pravdivosti, takže edituji. Jestli to tu ještě někdo čtete, dejte mi určitě nějak vědět :-). (Tipuji, že pokud se někdo ozve, bude to první Jelena, které nic neunikne. Tak jsem zvědavý :-).)

jelena · 28. 07. 2008 22:45

↑ BrozekP:

Děkuji moc za úplné a srozumitelné doplnění :-)

Kritický příspěvek jsem editovala a budu se snažit o vysoce odborné použití lopat (pokud si nebudu jistá, tak opět požádám o pomoc) - uznej, že zrovna tady jsem tak učinila (jinak by ta debata nebyla, že?)

Zdravim :-)

Pavel Brožek · 28. 07. 2008 23:02

↑ jelena:

Jsem moc rád, že moje poslední vysvětlení už je srozumitelné a problém se vyřešli ke spokojenosti všech :-) A ano, tady jsi tak učinila, jinak bych tento příklad asi přešel s tím mým prvním příspěvkem #37 :-).

matoxy · 30. 07. 2008 16:44 — Editoval matoxy (30. 07. 2008 17:16)

Zdravím,

Pozeral som si odvodenia pre výpočet derivácie elementárnej funkcie.
Na odkazovanej stránke mojaskola je výpočet derivácie konštantnej funkcie odvodený takto: $f'(x_0) =\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=\lim_{\Delta x \to 0}\frac{c-c}{\Delta x}=\lim_{\Delta x \to 0}\frac{0}{\Delta x}=0$ . Nie je to však nedefinovaný výraz: 0/0?

A ešte si neviem rady s odvodením y=sin x. Išiel som na to takto: $\lim_{\Delta x \to 0}\frac{\sin(x_0+\Delta x)-\sin x}{\Delta x}$ rozložil som podľa vzorca sin (x+y) a dosatal: $=\lim_{\Delta x \to 0}\frac{\sin{x_0}\cos{\Delta x}+\sin{\Delta x}\cos{x_0}-\sin{x_0}}{\Delta x}=\lim_{\Delta x \to 0}\frac{\sin{x_0}(\cos{\Delta x}-1)+\sin{\Delta x}\cos{x_0}}{\Delta x}$ . Ďalej však vôbec neveim ako to upravi?. Pozeral som aj v knihe od pána Jarníka, ale ani tam som to nepochopil, aj keď je to tam odvodené trochu inak.

Pavel Brožek · 30. 07. 2008 17:15

↑ matoxy:

ahoj, tady je to trochu jinak, nejde o nedefinovaný výraz. 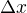$\Delta x$ je malé číslo, ale ne nula, protože limita nezávisí na funkční hodnotě v bodě v kterém ji počítáme. Nula dělená nenulovým číslem je nula, takže

$\lim_{\Delta x \to 0}\frac{0}{\Delta x}=\lim_{\Delta x \to 0}0=0$

Nedefinovaný výraz $\frac{0}{0}$ by vznikl, pokud bychom použili větu o limitě podílu, tedy

$\lim_{\Delta x \to 0}\frac{0}{\Delta x}=\frac{\lim_{\Delta x \to 0}0}{\lim_{\Delta x \to 0}\Delta x}=\frac{0}{0}$

Toto použití ale není správné, protože nejsou splněny předpoklady té věty - věta předpokládá, že limita ve jmenovateli je různá od nuly.

Navíc, pokud při počítání limit dostaneme nedefinovaný výraz, tak to neznamená, že limita neexistuje, ale musíme použít jiný postup.

matoxy · 30. 07. 2008 17:37 — Editoval matoxy (31. 07. 2008 16:23)

Jasné chápem a ešte by som rád vedel, ako sa odvodí vzorec pre derivovanie funkcie a^x.

Dostal som sa len k úprave $\lim_{\Delta x \to 0}a^{x_0} \cdot \frac{\large{a^^{\Delta x}}-1}{\Delta x}$ , ale neveim ako previes? $\lim_{\Delta x \to 0}\frac{a^{\Delta x}-1}{\Delta x}$ na $\ln a$ .
Mohly by ste vysvetli??

ttopi · 30. 07. 2008 17:49

K derivaci funkce $a^x$ jsem, našel toto:

matoxy · 31. 07. 2008 16:55

ttopi jasné chápem.

Marian · 31. 07. 2008 17:17 — Editoval Marian (31. 07. 2008 23:32)

↑ ttopi:

Ten naskenovany prispevek se mi prilis nelibi. Mam pro to hned nekolik dobrych dyuvodu.

(1) Ten trik, o kterem je rec, neni nic jineho nez definice mocniny a^x. Myslim, ze by zasluhovalo to prinejmensim pripomenout. Rozhodne bych to jako trik nenazval.

(2) Ve tretim radku od spodniho okraje je gramaticky nesmysl: "... s vnejsi funkci je ...".

(3) Dale absolutne nechapu, proc autor pouziva pro nasobeni v radku znaku "times" sazeneho jako $\times$ , ktery zde nema opodstatneni, navic z grafickeho hlediska je velmi nevyhodny pro moznou kolizi s oznacenim promenne, tj. s x.

K derivaci funkce a^x si radsi otevrete nejakou kvalitni ucebnici. Kritika samozrejme neni smerovana ttopimu, ale autorovi prispevku (snad to nepsal ttopi).

Pavel Brožek · 31. 07. 2008 17:47

Jinak se dá derivace spočítat ještě takto:

$(a^x)'=\lim_{\Delta x\to0}\frac{a^{x+\Delta x}-a^x}{\Delta x}=a^x\lim_{\Delta x\to0}\frac{a^{\Delta x}-1}{\Delta x}=a^x\lim_{\Delta x\to0}\frac{e^{\Delta x\ln a}-1}{\Delta x}=$

Použijeme substituci $y=\Delta x\ln a$

$=a^x\lim_{y\to0}\frac{e^{y}-1}{\frac{y}{\ln a}}=a^x\ln a\,\cdot\lim_{y\to0}\frac{e^{y}-1}{y}=a^x\ln a$

jelena · 31. 07. 2008 20:10 — Editoval jelena (01. 08. 2008 18:31)

↑ Marian:

Editace :-) tady jsem oznamovala, že se zajímámo skloňování :-)

ttopi · 31. 07. 2008 20:49 — Editoval ttopi (31. 07. 2008 20:50)

↑ Marian:
No... Je to zkopírované z nějakých online skript.
Gramatické chyby jsou všude, to bych nepovažoval za nějakou chybu v samotné derivaci, tam se jedná o něco jiného.
S tím "i" "í" to taky nechápu, já tam vidím funkcí, což je dobře.

Onen trik podle mě skutečně trikem je. Je to sice jednoduchá věc, nicméně každého by zřejmě nenapadlo to takto přepsat.

Marian · 31. 07. 2008 23:32

↑ jelena:↑ ttopi:

No mam starsi monitor, takze pismo je casto rozmazane. Ted vidim, ze je to O.K. Palny poplach. Provedu EDIT.

matoxy · 02. 08. 2008 01:01

Zdravím,

Príklad 13 od ttopiho som pochopil tak, že si môžeme z definície odvodi? ako sa derivuje e^x aj x a potom to použijeme pri odvodzovaní a^x. Odvodenie od BrozekaP však tiež nie je zložité a priame.

Mohol by ešte niekto prosím prepočíta? nasledovné príklady?
Lebo som ich vypočítal, ale každý mi vyšiel o trochu inak ako uvádzajú na stránke.

Príklad 21.) $y=\ln \frac{2-x}{2+x}$ $y'=(\ln y)'\cdot \left(\frac{2-x}{2+x}\right)'=\frac{1}{\frac{2-x}{2+x}}\cdot \frac{(2+x)'\cdot (2-x)-(2-x)'(2+x)}{(2+x)^2}$ ... po úpravách vyšlo: $4\cdot (4-x^2)^{-1}$ Uvádzajú však výsledok: $4\cdot (x^2-4)^{-1}$

Príklad 222.) $y=x\sqrt{1+x^2}$ upravil som to na $y=\sqrt{x^2+x^4}$ zaviedol som substitúciu: $t=x^4+x^2$ a derivoval: $y'=(t^{\frac12})'\cdot (x^4+x^2)'$ ... po úravách vyšlo $\frac{2(2x^2+1)}{\sqrt{x^2+1}}$ . Na stránke uvádzajú výsledok: $\frac{2x^2+1}{\sqrt{x^2+1}}$ .

Za pomoc ďakujem.

ttopi · 02. 08. 2008 01:10 — Editoval ttopi (02. 08. 2008 01:26)

↑ matoxy: Ta závorka se derivuje trošku jinak. Derivace čitatel * opíšu jmenovatel - opíšu čitatel * derivace jmenovatele, to celé lomeno jmenovatel na druhou. Pak vyjde opravdu $\frac{4}{x^2-4}$

ttopi · 02. 08. 2008 01:18

To druhý... $\frac{2x+4x^3}{2\sqrt{x^2+x^4}}=\frac{2x(1+2x^2)}{2x\sqrt{x^2+1}}= \frac{2x^2+1}{\sqrt{x^2+1}}$

matoxy · 02. 08. 2008 23:25

ttopi, ten prvý príklad som spravil chybu v tom, že som si neuvedomil, že nie je jedno, ktorú funkciu zderivujem v prvom sčítanci a ktorú v druhom. Pri súčine funkcií je to totiž jendno, pretože pri derivácií je tam súčet dvoch súčinov funkcií, a tam som si na to zvykol, že som nedával pozor, ktorú funkciu dám prvú a ktorú druhú. Pri derivácií podielu funkcií je však v čitateli mínus a keď som na to nedal pozor, spravilo to šarapatu. V druhom som zas pri derivovaní t^{1/2} zabudol pripísa? 1/2 pred t a potom mi tam v menovateli chýbala 2. Ale už je to ok.

matoxy · 05. 08. 2008 19:33

Znova by som rád pomôc? s nejakými príkladmi.

93.) Těleso sjede po nakloněné rovině 50 m dlouhé za 10 s. Předpokládáme-li, že dráha je kvadratickou funkcí času a že počáteční rychlost tělesa je rovna nule, jaká je jeho konečná rychlost?

Počítal som to takto: Kďže prvá derivácia dráhy podľa času je okamžitá rýchlos? tak môžeme písa?: $s=at^2$ , z čoho po dosadení dostaneme $a=\frac{s}{t^2}=0,5$
Keďže máme a, môžeme dosadi? do 1. derivácie dráhy $s'=2at=v$ , teda $v=2\cdot 0,5\cdot 10=10ms^{-1}$ . To je výsledok, ktorý uvádzajú aj na stránke, len si nie som istý či je to dobrý postup, pretože kvadratická funkcia je aj ax^2+bx + c nie?

príklad 96.) Vlak se rozjíždí ze stanice pohybem vyjádřeným rovnicí s = at^2 + bt + c a po uplynutí jedné minuty dosáhne rychlosti 60 km/h. Jak velkou vzálenost ujede, než této rychlosti dosáhne? Jaké je zrychlení onoho pohybu?

Tento príklad som sa snažil rieš? podobne no Akosi mi tam čosi chýba, pretože keď som skúsil počíta? podľa toho, že zrýchlenie je 2. deriváciou dráhy podľa času tak som dostal rovnicu $s''=2a$ a to je rovnica s dvoma neznámimi nie?

jelena · 07. 08. 2008 13:04

↑ matoxy:

Zdravím :-)

využívám polední přestavku a napíší něco, co se bude zdát jako hodně velká lopata a tak k tomuto textu prosím přistupovat :-)

Nevím, zda je to přesně to, co potřebuješ, případně upřesní, prosím.

93) Těleso sjede po nakloněné rovině 50 m dlouhé za 10 s. Předpokládáme-li, že dráha je kvadratickou funkcí času a že počáteční rychlost tělesa je rovna nule, jaká je jeho konečná rychlost?

Nejsem si úplně jistá, zda rozumím, z čeho pramení otázka na závěr tvého výpočtu. Možná trochu váháš, zda vzorec, co umíme z fyziky pro rovnoměrně zrychlený pohyb, odpovídá tomu vzorci, který se tváří jako kvadratická funkce?

Pokud počítáš tak, jak máš v příspěvku, tak a není zrychlení, ale nějaký koeficient u kvadratického členu kvadratické funkce. Aby nedocházelo k matení pojmu, použila bych jiná písmenka pro označení koeficientů:

třeba tak: f(t)=kt^2+qt+p. Potom je celý tvůj postup v pořádku.

Že zápis kvadratické funkce není totéž (na pohled) jako vzorec z fyziky?

Já se pokusím napsat svůj polopatický způsob pro to, jak nahlížet na kvadratickou funkci pro vyjádření rovnic rovnoměrně zrychleného pohybu:

Předpokládejme, že na základě měření nebo prohlášením důvěryhodné osoby se zjistilo, že závislost dráhy na čase je kvadratická funkce, její obecný zápis bude:

f(t)=kt^2+qt+p,

ze zvyku použijeme toto označení: s= f(t), potřebujeme ještě najit „fyzikální smysl“ koeficientů k, q, p (záměrně jsem opět nepoužila a)

p: absolutnímu členu p budeme říkat počáteční vzdálenost s_0

první derivace drahy v =f´(t)=2kt +q absolutnímu členu q budeme říkat počáteční rychlost v_0

druha derivace drahy je zrychlení a=f´´(t) = 2k, odsud můžeme najit koeficient k=a/2

Teď to projdeme nazpátek a „vytvoříme vzorce“ v takových písmenkách jako ve fyzice.

v =2*(a/2)*t+v_0=at+v_0
s= (a/2)*t^2+v_0*t+s_0 – to je vzorec, který umíme pro rovnoměrně zrychlený pohyb s počáteční rychlosti a s počáteční vzdálenosti.

Já osobně úplně nejraděj odvozuji vzorce pro rovnoměrně zrychlený pohyb pomoci integrace konstanty a (zrychlení) po dt (integrovat konstantu umím a zbytek už si odvodím 

96) Vlak se rozjíždí ze stanice pohybem vyjádřeným rovnicí s = at^2 + bt + c a po uplynutí jedné minuty dosáhne rychlosti 60 km/h. Jak velkou vzdálenost ujede, než této rychlosti dosáhne? Jaké je zrychlení onoho pohybu?

60 km/h = 1 km/min (jen to vhodně převedu, jinak pozor na jednotky)

Tady je potřeba začít od 1. derivace funkce s = kt^2 + qt + p (vidíš, opět jsem přepsala koeficienty)

s´= 2kt + q, v označení zvyklém máme v= 2kt+v_0 (v_0=0), odsud hledáme koeficient k:

1=2k*1, k=0,5 (není to ovšem zrychlení)

p = s_0=0, q = v_0=0, k=0,5 – půjdeme to dosadit do kvadratické funkce a dostaneme>
s=0,5t^2, pro čas 1 minuta mame s = 0,5 km.

Zrychlení dopočitej sám.

Na strankách pana Reichla http://www.jreichl.com najdeš hodně pěkných materiálů a také matematiku pro fyziky:

http://www.jreichl.com/fyzika/vyuka/tex … matika.pdf doporučuji také se pokusit nekteré vztahy odvodit i tak, jak jsem prováděla.

Odkaz na stranky pana Reichla je zaroveň takovým letním pozdravem pro kolegu, který tady ted moc nebyvá, ale snad se ten pozdrav k nemu dostane.

matoxy · 09. 08. 2008 16:59 — Editoval matoxy (10. 08. 2008 10:49)

Zdravím,
neviem síce ako vyzerá text, keď vyzerá ako lopata:), ale pokúsil som sa ten váš pochopi? a hádam aj celkom úspešne.

Postup k príkladu č.93.)

s=50m
t=10s
v=? (s') okamžitá rýchlos?
$s=kt^2+px+q$
Platí: $s''=2k=a\Rightarrow k=\frac a2$ a $s=\frac12 at^2\Rightarrow a=\frac{2s}{t^2}$ .
Z čoho dostávame $k=\frac{s}{t^2}$ .
$s'=2kt+p=v_0$ Ak p je počiatočná rýchlos?, tak z toho dostávame $v_0=2\frac{s}{t^2}t=\frac{2s}{t}=10m\cdot s^{-1}$

Myslím, že teraz je ten postup už v poriadku, len by som mal otázku k členom p a q. To, že člen p je počiatočná rýchlos? a q je počiatočná dráha by sme mohli zisti? tak, že by sme sledovali "správanie" paraboly pri dosadzovaní rôznych dôležitých čísel za členy p a q?

96.) Zrýchlenie by išlo dopočíta? takto: $s=\frac12 at^2\Rightarrow a=\frac{2s}{t^2}=0,27m\cdot s^{-1}$ . Len sa mi na tom nepáči to, že tam vôbec netreba derivácie a nejak ma nenapadá ako by mi pri tom mohly pomôc?.

EDITACE: Čo sa týka stránok pána Reichla, tak som ich už videl (zrejme odkazované niekde tu) a ten text tiež, len neviete či nie je vydaný aj v tlačenej, knižnej podobe?

jelena · 10. 08. 2008 12:30

matoxy napsal(a):
ako vyzerá text, keď vyzerá ako lopata:)

No, vyzerá tak, že keď by ho pozreli matematici z fora, tak by vraveli: "Jelena, takto jednoducho to predsa nie, grrrrr"

Byla to trochu taková hra s kvadratickou funkci a derivaci :-)

matoxy napsal(a):
k príkladu č.93.)
len by som mal otázku k členom p a q. To, že člen p je počiatočná rýchlos? a q je počiatočná dráha by sme mohli zisti? tak, že by sme sledovali "správanie" paraboly pri dosadzovaní rôznych dôležitých čísel za členy p a q?

V podstatě ano, raděj bych viděla toto:

zkus nakreslit graf konstantní gunkce f(t)=a - ten bude znazorňovat, že zrychlení při rovnoměrně zrychleném pohybu je konstantní. A pak si polozit otazku - jak vypadala funkce v(t), že když jsme v(t) zderivovali, tak nam vznikla funkce f(t) = a

v(t)=???, v´(t)=a

A stejným způsobem přejdi od v(t) k s(t) - pak porovnej zápis funkce s(t) s obecným zápisem kvadratické funkce.

matoxy napsal(a):
96.) Zrýchlenie by išlo dopočíta? takto: $s=\frac12 at^2\Rightarrow a=\frac{2s}{t^2}=0,27m\cdot s^{-1}$ . Len sa mi na tom nepáči to, že tam vôbec netreba derivácie a nejak ma nenapadá ako by mi pri tom mohly pomôc?.

Ale k tomuto vzorci jsme došli právě pomoci derivace - pokud projdes jeste jednou můj postup k 93 - je videt, kde vzniklo 1/2at^2 (mám kontrolovat i číselný výsledek, nebo už kontrolováno?)

matoxy napsal(a):
...stránok pána Reichla, ten text tiež, len neviete či nie je vydaný aj v tlačenej, knižnej podobe?

O vydání přímo materiálu od pana Reichla (matematika pro fyziky) - asi ne, nenarazila jsem na něco takového, ale jiné knihy s problematikou matematiky pro fyziky se daji sehnat, treba:

http://www.vuv.cz/knihovna/l.dll?cll~32913

Od pana Reichla mám knihu "Klič k fyzice" - je zábavná a polopatická :-)

(jinak já používám zdroje v ruštině - hodně z http://eqworld.ipmnet.ru/ru/library.htm, ale to asi moc nepomůže, až časem, že?)

Matematické Fórum

#51 28. 07. 2008 21:06 — Editoval jelena (28. 07. 2008 22:32)

Re: Limity

#52 28. 07. 2008 21:35

Re: Limity

#53 28. 07. 2008 21:48

Re: Limity

#54 28. 07. 2008 21:55

Re: Limity

#55 28. 07. 2008 22:15 — Editoval BrozekP (12. 11. 2010 22:44)

Re: Limity

#56 28. 07. 2008 22:45

Re: Limity

#57 28. 07. 2008 23:02

Re: Limity

#58 30. 07. 2008 16:44 — Editoval matoxy (30. 07. 2008 17:16)

Re: Limity

#59 30. 07. 2008 17:15

Re: Limity

#60 30. 07. 2008 17:37 — Editoval matoxy (31. 07. 2008 16:23)

Re: Limity

#61 30. 07. 2008 17:49

Re: Limity

#62 31. 07. 2008 16:55

Re: Limity

#63 31. 07. 2008 17:17 — Editoval Marian (31. 07. 2008 23:32)

Re: Limity

#64 31. 07. 2008 17:47

Re: Limity

#65 31. 07. 2008 20:10 — Editoval jelena (01. 08. 2008 18:31)

Re: Limity

#66 31. 07. 2008 20:49 — Editoval ttopi (31. 07. 2008 20:50)

Re: Limity

#67 31. 07. 2008 23:32

Re: Limity

#68 02. 08. 2008 01:01

Re: Limity

#69 02. 08. 2008 01:10 — Editoval ttopi (02. 08. 2008 01:26)

Re: Limity

#70 02. 08. 2008 01:18

Re: Limity

#71 02. 08. 2008 23:25

Re: Limity

#72 05. 08. 2008 19:33

Re: Limity

#73 07. 08. 2008 13:04

Re: Limity

#74 09. 08. 2008 16:59 — Editoval matoxy (10. 08. 2008 10:49)

Re: Limity

#75 10. 08. 2008 12:30

Re: Limity

matoxy napsal(a):

matoxy napsal(a):

matoxy napsal(a):

matoxy napsal(a):

Zápatí