Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninová limita (TOTO TÉMA JE VYŘEŠENÉ)
#2 16. 07. 2008 13:28
Re: Prázdninová limita
Zdravim Pavle!
Cekal jsem, az se ukazes na tomto foru. Myslim, ze tva ucast zde bude velkym prinosem, nicmene nechci predjimat. Ted se tady na foru nic moc nedeje, ale mozna se nekdo najde, aby se popral s limitou vyse. Protoze jeji reseni znam, prenecham uvahy ostatnim, popr. se pokusim o pripadne nasmerovani nebo opravu, pokud me nepredbehnes ovsem.
Offline
#3 16. 07. 2008 17:36
Re: Prázdninová limita
Myslím Mariane, že na chvíli necháme příklad pro ostatní uležet a dozrát :-) Určitě někdo příjde s řešením.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 16. 07. 2008 19:24
Re: Prázdninová limita
Pozor na to, že s nekonečnem nelze počítat stejně jako s reálnými čísly. Konkrétně výraz  se nedefinuje vzhledem k tomu, že může nabývat de facto libovolné hodnoty. Viz např.
se nedefinuje vzhledem k tomu, že může nabývat de facto libovolné hodnoty. Viz např. nebo
nebo 
Limity jsou různé, přestože obě vedou na výše uvedený neurčitý výraz. Nahradíme-li čitatel ve zlomku jakýmkoliv reálným číslem, pak výraz  může nabývat opravdu libovolné hodnoty. Proto nelze předem tvrdit, že
může nabývat opravdu libovolné hodnoty. Proto nelze předem tvrdit, že  je 0.
je 0.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 17. 07. 2008 01:07 — Editoval Marian (17. 07. 2008 01:07)
Re: Prázdninová limita
↑ matoxy: Slovo pomoct je natolik relativni zalezitosti, ze me prepada spise skepse. Pokud bys aplikoval na clen (1+1/n)^n binomicky rozvoj, stale se budes potykat s Eulerovym cislem e, jez figuruje v zadani, tudiz si nepomuzes de facto.
Offline
#9 17. 07. 2008 09:13
Re: Prázdninová limita
↑ ttopi: Nemas pravdu. Pravdepodobne jsi nezaregistroval, ze musis brat potencialni x --> +oo. V podstate bys musel hledat vodorovnou asymptotu. A pro kladna realna cisla x je patrne, ze by se to mohlo stat.
Ale o vztahu limity posloupnosti a limity funkce v nevlastnim bode bychom mohli diskutovat.
Offline
#10 17. 07. 2008 09:16
Re: Prázdninová limita
Graf je celý jen pro orientaci, ale samozřejmě, že řešením jsem myslel tu pravou červenou "čáru", která si myslím, že do - nekonečna jde.
Na papíře mám 2 jakási početní řešení, která dávají také -nekonečno, ale je otázkou, zda jsou správná.
oo^0 = 1
Offline
#11 17. 07. 2008 09:27 — Editoval Marian (17. 07. 2008 11:59)
Re: Prázdninová limita
↑ ttopi: V tom pripade bys patrne mohl podobne argumentovat i tehdy, kdybys uvazoval funkci f(x):=1/x. Ta funkce je klesajici, tedy limita (pro x --> +oo) bude -oo, i kdyz 1/x>0 pro kladna x. Nevim, co pak beres jako meritko pro to, abys v relativne nepruhlednem prikladu limity dokonce tvrdil, ze posloupnost bude klesajici. A z toho, resp. z graficke interpretace jeste dedukovat, ze tato limita je nevlastni.
Toto neni seriozni pristup studenta matemtiky (jak se jiste shodneme), ale na druhou stranu nektere graficke interpretace dokazou poukazat na moznou cestu dukazu. Tady dokonce geometricka interpretace vyvraci tvuj nazor o tom, ze limita studovane posloupnosti je nevlastni, nebot i pro velke zmeny hodnot n dostavas "male" zmeny pro hodnoty posloupnosti.
Offline
#15 17. 07. 2008 13:22
Re: Prázdninová limita
↑ ttopi:
(1) Chtel jsem, at podobne zareagujes na mou poznamku, protoze ja se musim uplne stejne divit, odkud ty beres, ze z tveho grafu vyse je limita -oo. Nevidim ten duvod stejne jako ty nevidis duvod, proc by melo platit lim_{x --> +oo}1/x= -oo. A pritom ty grafy vypadaji dosti "podobe". Zkus si nakreslit treba graf funkce f(x):=(1/x)-1 pro kladna x. Dostanes dosti podobny obrazek jako v pripade tveho grafu vyse. A nic podobneho se o nevlastni limite soudit neda; plati totiz lim_{x --> +oo}((1/x)-1)=-1.
Co tim chci tedy rici. Nemuzu z grafu funkce korektne dedukovat jeji vlastnosti, natoz vlastnosti v nevlastnim bode.
(2) "Z grafu je videt" ... (doplnit si muzes sam, tak jak jsi treba zvykly). Ono z grafu neni videt nic, co se limity v nevlastnim bode tyce. Muzeme pouze hypoteticky usuzovat a treba ziskat tak nejakou domenku, kterou pozdeji jsme treba schopni i dokazat.
Vubec nemyslim sve prispevky proti tobe, pokud vyznely spise negativne.
Offline
#18 17. 07. 2008 15:10 — Editoval Marian (17. 07. 2008 15:12)
Re: Prázdninová limita
↑ pathconf:
Problem je v tom, ze ti tam vyika neurcity vyraz (1+0)^(oo), tedy v postate "jedna na nekonecno" a to se vubec nemusi rovnat jednicce, tedy tvuj vypocet zhorel na trivialni limite, nebot se da ukazat, ze plati
kde "e" je tzv. Eulerovo cislo (zklad prirozenych logaritmu).
Offline
#19 17. 07. 2008 15:32 — Editoval ttopi (17. 07. 2008 16:01)
Re: Prázdninová limita
Já vymyslel toto, nicméně to bude asi špatně.
1.postup:
Roznásobil jsem závorku na n-tou a pak jen upravoval.
2.postup:
Za pokus nic nedám:-)
Marian: Ten graf je, když tam dám větší rozpětí X ještě méně čitelnější, nicméně i z tohoto vidím, že by to mělo jít do -nekonečna.
Graf neměl znamenat řešení. Vím ze zkušenosti, že učitele vyžadují početní postup. Toto bylo jen pro ilustraci. Co se týče limity (1/x)-1, tak tam bych vyšel z limity 1/x a pouze bych odečetl 1, určitě bych tedy netvrdil, že pujde do -nekonečna, ale to teď není podstatné. Když už to bereš takto vážně, tak bych pak mohl s trochou nadsázky tvrdit, že podle grafu nemůžeš jednoznačně říct, že limita x^2 pro x jdoucí do +nekonečna je +nekonečno, protože v grafu to nekonečno není vidět a tudíž nemohu říci, jak tam graf bude vypadat. Já z uvedeného grafu vidím, že to jde do -nekonečna (pokud je výsledek špatně, tak to řekni a já sklopím uši), ačkoli je ten graf vidět jen do x=50.
oo^0 = 1
Offline
#20 17. 07. 2008 15:43 — Editoval Marian (17. 07. 2008 15:52)
Re: Prázdninová limita
↑ ttopi:
Ad 1. Neni mi jasne, jak jsi provedl ono umocneni. Navic prvni rovnitko nemuze platit, protoze - jak pisi v prispevku #18 - je
Pro tvuj upraveny clen ale plati (podle tebe - ovsem je to spatne, to muzes videt o radek vyse)
Ad 2. Nelze psat dokonce ani toto
Takze te musim opet zklamat, ale ani jedna z tebou navrhovanych moznosti neni spravne.
Offline
#22 17. 07. 2008 15:56 — Editoval Marian (17. 07. 2008 15:58)
Re: Prázdninová limita
↑ ttopi: To umocneni podle tebe je spatne. Musis pouzit binomickou vetu. Pak bude
A pokud je cosi "nekonecno*nula", pak se musi pouzit jina vhodna uprava. Kazdy takovyto vyraz se da pak prevest na 0/0, resp. oo/oo. Snad by toto mohlo trochu pomoci.
Dale si v prispevku #19 oprav pod symboly "lim" x na n.
Offline
#24 17. 07. 2008 16:25
Re: Prázdninová limita
↑ ttopi:
l'Hospitalovo pravidlo jsem zamerne nevyrkl. A pozor take na puvodni zadani; ono v puvodnim zadani nejou dve "ecka" a to je podstatny rozdil.
No, jeste mame pred sebou poradny kus pocitani.
Offline
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninová limita (TOTO TÉMA JE VYŘEŠENÉ)



 , keď n->oo?
, keď n->oo?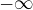 .
.