Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninová limita (TOTO TÉMA JE VYŘEŠENÉ)
#28 23. 07. 2008 20:38
Re: Prázdninová limita
Zdravím všechny, vidím, že limita je opravdu oříšek. A tak je to správně :-) Takže uvedu několik prvních kroků, snad to pomůže. Nejdříve zavedu substituci n=1/x, pak limitu vyjádřím pomocí nové proměnné x a nakonec přepíšu mocninu vhodnějším způsobem. 
Zbytek někdy příště :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#29 23. 07. 2008 22:49 — Editoval kaja.marik (23. 07. 2008 22:49)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Prázdninová limita
Zdravim, vzpomnel jsem si po precteni toho predchoziho prispevku na diskuse okolo limity posloupnosti a funkce, napriklad zde, ale i jinde :)
----------------------------------------------
Maminka hajná, když se Kája blížil k domovu, si zpívala. Kája ani honem nepoznal, kterou, jakou měl radost, že maminka zpívá. „Má zlatá maminko, to jsem vás už dlouho neviděl!“ „A to jistě máš něco za lubem, když jdeš s takovou,“ smála se maminka, přitiskla ho k sobě a pohladila po hlavě.
Offline
#30 24. 07. 2008 18:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
↑ Pavel:
tak pokračování:
podle L'Hospitalova pravidla je
z aritmetiky limit a jednodušší limity  (jednoduše řešitelná jako limita složené funkce + L'Hospital nebo se to dá jednoduše převést na známou limitu
(jednoduše řešitelná jako limita složené funkce + L'Hospital nebo se to dá jednoduše převést na známou limitu  ) máme s Taylorovým rozvojem pro
) máme s Taylorovým rozvojem pro 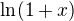 v okolí nuly
v okolí nuly
Všechny předpoklady použitých vět byly splněny (kdo nevěří, ověří), takže původní limita je opravdu  .
.
Doufam, že jsem někde neudělal nějakou hloupou chybu :-)
Offline
#31 24. 07. 2008 21:17
Re: Prázdninová limita
Výborně, tak jsme se dočkali !!!. To je ono. Ukážu ještě jeden postup:
položíme-li  , pak pro
, pak pro  platí, že
platí, že  a můžu tedy psát
a můžu tedy psát
užitím l'Hospitalova pravidla dostávám výsledek
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#32 24. 07. 2008 21:31
Re: Prázdninová limita
Podobným způsobem je možné počítat limitu. Místo rozdílu je v ní podíl. O to je to jednodušší.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#33 27. 07. 2008 13:59
- Technik
- Zelenáč

- Příspěvky: 3
Re: Prázdninová limita
Ahoj. Mě vyšlo 
Když jsem nešťastným, pracuji na matematice, abych se stal šťastným. Když jsem šťastný, dělám matematiku, abych tak zůstal.
Fyzika-Matematika UJEP
Offline
#34 27. 07. 2008 14:13 — Editoval BrozekP (27. 07. 2008 16:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
↑ Technik:
Ahoj, mě to vyšlo  , ale tipuju, že si to omylem místo umocnění vynásobil, ne? :-)
, ale tipuju, že si to omylem místo umocnění vynásobil, ne? :-)
EDIT: Teď jsem si všiml, že  je správná odpověd na původní limitu, na tu už jsem zapomněl a řešil další :-) Takže se omlouvam.
je správná odpověd na původní limitu, na tu už jsem zapomněl a řešil další :-) Takže se omlouvam.
Offline
#35 27. 07. 2008 14:49
Re: Prázdninová limita
Výborně, -1/2 bude v mocnině e. Na základě tohoto výsledku se dají vytvářet další limity:
:-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#36 27. 07. 2008 16:36
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
↑ Pavel:
No dobře, abychom to tady neřešili do nekoncečna, vyřešim to všechno najednou :-)
Funkce 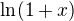 má Taylorův rozvoj (koeficienty označím
má Taylorův rozvoj (koeficienty označím  ):
):![kopírovat do textarea $\ln(1+x)= x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \frac{x^5}{5} - \dots = \sum_{n=1}^\infty a_nx^n = \sum_{n=1}^\infty {(-1)}^{n+1} \frac{x^n}{n} \; \mbox{ pro } x \in (-1,1]$](/mathtex/4a/4ac1084f8f85d009dce65d4682854ab5.gif)
Zavedu nyní posloupnosti  (i značí člen posloupnosti, j o kolikátou poslopnost se jedná) a přirozené logaritmy jejich limit:
(i značí člen posloupnosti, j o kolikátou poslopnost se jedná) a přirozené logaritmy jejich limit:
A nyní indukcí dokážu  :
:
1.  (jak je zřejmé z definice e)
(jak je zřejmé z definice e)
2. Předpokládáme, že  pro všechna
pro všechna  . Potom
. Potom
Takže kdybys chtěl tvořit limity dalších stupňů, tak to jsou exponenciely koeficientů Taylorova rozvoje funkce  . Doufám, že to nejde ukázat nějak triviálně, když jsem se s tim takhle vypisoval :-)
. Doufám, že to nejde ukázat nějak triviálně, když jsem se s tim takhle vypisoval :-)
Offline
#37 27. 07. 2008 17:04 — Editoval BrozekP (27. 07. 2008 17:05)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
Tak ještě zbývá vyřešit limitu
a další limity sestrojené z předchozích limit.
Můj odhad je, že to budou opět koeficienty rozvoje 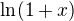 , tentokrát násobené e.
, tentokrát násobené e.
Offline
#38 27. 07. 2008 21:27
Re: Prázdninová limita
Tak jsem tu limitu počítal, žádná krása - substituce x=1/n, 2 krát l'Hospital, Taylorův rozvoj ln(1+x) a vyšlo  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#39 27. 07. 2008 21:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
Tak to se radujme, takový divný číslo, to musíme najít další :-) A zjistit co je to za divnou posloupnost :-)
Offline
#40 27. 07. 2008 23:22 — Editoval Pavel (27. 07. 2008 23:24)
Re: Prázdninová limita
Napadlo mě udělat Taylorův rozvoj funkce  v bodě a=0. Protože je výpočet derivací dosti divoký, vypomohl jsem si Maplem 11. A tady je výsledek:
v bodě a=0. Protože je výpočet derivací dosti divoký, vypomohl jsem si Maplem 11. A tady je výsledek:
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#41 28. 07. 2008 00:04
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
↑ Pavel:
No to je hezký :-) Je dobře vidět jak ten vnitřek limity vždycky požere ty členy rozvoje s nižší mocninou a u vyšších zase zbude x, který jde do nuly :-)
Ale jak bys ten rozvoj sestavil na papíru? Rozvoj se přece dělá tak, že počítáš ty koeficienty, tj dosadíš bod a=0 do nultý, první, druhý, ... derivace, ale to tady nejde, protože funkce ani žádná její derivace neni definovaná v nule. Takže kde ty koeficienty Maple vezme?
Offline
#42 28. 07. 2008 14:18
Re: Prázdninová limita
Já bych spojitě dodefinoval funkci  v 0 -
v 0 -  . Pak už bych derivace v bodě 0 počítal podle definice
. Pak už bych derivace v bodě 0 počítal podle definice . Znám-li první derivaci v 0, šel bych k derivacím vyšších řádů.
. Znám-li první derivaci v 0, šel bych k derivacím vyšších řádů.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#43 28. 07. 2008 15:25
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
To jsou ale přesně ty limity, co jsme řešili, takže jsme si tim nepomohli.
Offline
#44 28. 07. 2008 17:54
Re: Prázdninová limita
Zdravim asi po 2 mesicich me absence....mam asi spoooustu neomluvenych hodin, co? Technika zklamala :-( Jsem rada, ze se tu nezahali ani o prazdninach.
Diky za prikladek, ja tu puvodni limitu nakonec zkrotila i bez Taylorova rozvoje klasickym L'Hospitalem ;-) Jako trenink po 2 letech na matersky supr :-))
Offline
#45 28. 07. 2008 20:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
Tak k těm koeficientům rozvoje  se dá dostat i jinak, než počítáním těch hrozných limit: rozvinu logaritmus do řady, vytknu e, rozvinu do řady exponencielu a mám rozvoj do libovolného řádu:
se dá dostat i jinak, než počítáním těch hrozných limit: rozvinu logaritmus do řady, vytknu e, rozvinu do řady exponencielu a mám rozvoj do libovolného řádu:




Offline
#47 28. 07. 2008 20:53 — Editoval Marian (28. 07. 2008 20:54)
Re: Prázdninová limita
↑ BrozekP:
Mozna cesta vede i pres pouziti vety o binomicke rade. Plati totiz pro vsechna nenulova x
Po uprave je rozvoj obdobny jako u BrozekP.
Offline
#48 29. 07. 2008 19:50 — Editoval BrozekP (29. 07. 2008 19:58)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová limita
↑ Pavel:
Podle programu Mathematica:

Řekl bych, že to Mathematica jen neumí. Počítat se mi ta limita ale vůbec nechce :-) Takhle můžeš sestavit spoustu různých limit, ale hledat obecný způsob jak ty limity vyčíslit se mi už nechce :-) (bude to asi o dost těžší než předchozí příklady)
EDIT: Pokud snad nechceš v těchto limitách pokračovat (já myslím, že jsme si jich užili dost), tak navrhuji, abys zadal další prázdninový příklad :-) Třeba nějaký hezký prázdninový integrál :-) Nebo prázdninovou diferenciální rovnici. (Procvičení těchto oblastí by se mi hodilo i ke zkoušce, kterou budu dělat v září, z limit už zkoušku mám :-)
Offline
#49 29. 07. 2008 21:49
Re: Prázdninová limita
Já myslím, že těchto limit už bylo dost. Ani bych se nesnažil najít nějaké obecné odvození pro poslední typ. Mrknu se ještě na tu poslední. Něco vymyslím a když mě něco napadne, založím nové téma :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#50 31. 07. 2008 00:27
Re: Prázdninová limita
Ahoj. K tomu tvému poslednímu problému. Mathematica umí spočítat všechny typy limit, které si vymyslíš. Limity totiž nejsou tak komplikované jako integrály a existuje deterministický postup, kterým vyřešíš každou limitu (Taylor, je prasácký, ale vždy vede do cíle). Konkrétně v tom co si napsal je v pořádku, jak to vyšlo. Očekáváš asi výsledek 1 a možná tě nepřekvapí, když řeknu že absolutní hodnota z výsledku je 1 a celé číslo je komplexní. Pokud bys výraz uvnitř bral jako posloupnost, pak jednoduše bude neabsolutně divergovat (konkrétně oscilovat).
1 + 1 = 1 + 1
... a nebo taky ne
Offline
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninová limita (TOTO TÉMA JE VYŘEŠENÉ)

