Matematické Fórum

Pavel Brožek

↑↑ rughar:
Výsledek 1 neočekávám, podle grafu funkce očekávám číslo z intervalu $(0,64\,;\,0,645)$ (používám substituci $x=\frac{1}{n}$ a tedy hledám limitu v nule)

A pokud řekneš, že absolutní hodnota z výsledku je 1 a celé číslo je komplexní, tak to mě překvapí, protože pokud existuje limita reálné funkce/posloupnosti, pak má vždy nulovou imaginární část. A pokud by limita byla komplexní číslo s absolutní hodnotou 1, pak to není ComplexInfinity (komplexní nekonečno). Oscilovat posloupnost nebude, protože je monotónní.

Pokud snad něco z toho co jsem napsal není správně, tak mi prosím podrobněji vysvětli svá tvrzení.

Cheop · 31. 07. 2008 12:35

Kleinova lahev

Marian · 31. 07. 2008 12:36

↑ Cheop:

Jeste nam Pavel ukaze, jak to v tom pekle staceji do Kleinovych lahvi a budu spokojeny
:-)

rughar · 31. 07. 2008 13:03 — Editoval rughar (31. 07. 2008 13:05)

↑ BrozekP:

Nejsem si teď moc jist, co má s posledním příspěvekem společná substituce x = 1/n. Každopádně když s dívám na ten tvůj graf, pak to svědčí o tom, že jsi ji použil nesprávně.

Existuje matematická věta, která říká, že pokud

$\lim\limits_{n \to n_0}f(n)=x_0$
$\lim\limits_{x \to x_0}g(x)=A$

pak

$\lim\limits_{x \to x_0}g(f(n))=A$

Takhle se používá susbstituce. V tvém případě je tedy f(n) = 1/n. Tahle matematická věta lze použít jen zehdy pokud je splněn alespoň jeden z následujících předpokladů.

1. f(n) je spojitá kolem bodu n0. Což není pravda, protože v našem případě je n0 rovno 0 a v 0 je 1/n nespojité

2. Pro g(x) platí, že existuje takové q, že na intervalu $x\in(x_0-q;x_0+q)$ platí, že g(x) nabývá různých hodnot pro různá x (čili je monotóní a nesmí to být konstatní funkce). Což v tvém případě, když se tak dívám na ten tvůj graf nebude asi pravda. A? už zvloíš libovolně malé okolí kolem 0, nikdy to na něm nebude zjevně monotóní (g(x) může nabývat stejných hodnot pro různá x)

Substituce je velmi často příliš naivní krok právě proto, že velmi často svádí použít 1/x, která ale hned první z těch uvedeých předpokladů. Člověk musí mít tedy vědomí o tom druhém předpokladu, který vypadá sice dost složitě, ale po hlubším prozkoumání celkem logicky.

A co se týče toho komplexního výsledku, pak například funkce (-1)^x vypadá v komplexním oboru takto:

$\pi(\cos(x)+i\sin(x))$

O čemž lze říci, že absolutně konverguje k 1 (absoutní hodnota je stále 1), ale ve skutečnosti to diverguje (osciluje). Takhle jsem to v předcházejícím svém příspěvku myslel. A to si přesně myslím že něco podobného u té poslední limity vychází.

Marian · 31. 07. 2008 13:33 — Editoval Marian (31. 07. 2008 13:36)

↑ rughar:

Budu reagovat pouye na ten zaver. Pravdu nemas, protoze s (-1)^x je to takto:

$(-1)^x:=e^{x\cdot {\mathrm{Ln}}\, (-1)}, \qquad\mathrm{kde}\qquad {\mathrm{Ln}\, (-1)}=(2k+1)\pi\mathrm{i},\quad k\in\mathbb{Z}.$

Tedy je za predpokladu, ze $x=a+b\mathrm{i},\quad (a,b)\in\mathbb{R}^2$

$(-1)^x=e^{x\cdot (2k+1)\pi\mathrm{i}}=e^{(a+b\mathrm{i})(2k+1)\pi\mathrm{i}}=e^{a(2k+1)\pi\mathrm{i}}\cdot e^{-b(2k+1)\pi}.$

Nicmene podle tveho plati

$|(-1)^x|=|\pi (\cos x+\mathrm{i}\cdot\sin x)|=\pi\neq 1.$

Tedy je spravne pro x:=a+bi, a,b realna libovolna cisla

$|(-1)^x|=e^{-b(2k+1)\pi},\qquad k\in\mathbb{Z}.$

nebo take

$|(-1)^x|=e^{(2k+1)\pi\cdot\Im (-x)}.$

Pro hlavni hodnotu pak staci uvazit k=0.

rughar · 31. 07. 2008 13:41

Uh. Máš pochopitelně pravdu. Málo jsem se zamýšlel. Tvůj výsledek je správně. Zapsáno v goniometrickém tvaru to mělo být

$\cos(\pi x)+i\sin(\pi x)$

Pavel · 31. 07. 2008 13:45

↑ rughar:

U třetí limity shora by mělo být $n\to n_0$ .

Pokud jde o substituci, stačí mnohem jednodušší podmínky, které v tomto případě splněny jsou.

Je-li

$\lim\limits_{n \to n_0}f(n)=x_0\nl \lim\limits_{x \to x_0}g(x)=A$

a platí-li pro všechny body n z nějaké prstencové okolí bodu $x_0$ (okolí neobsahující bod $x_0$ )

$f(n)\,\neq\, x_0$ , pak

$\lim\limits_{n \to n_0}g(f(n))=A$

Marian · 31. 07. 2008 13:46 — Editoval Marian (31. 07. 2008 13:47)

↑ rughar:

Souhlasim, ale jen castecne. Tvuj pripad pak neresi situaci, kdyz $x\in\mathbb{C}\setminus\mathbb{R}$ . Ale to jsem jiz napsal ja. Chci upozornit na to, ze absolutni hodnota vyrazu (-1)^x, pro nerealna cisla x neni rovna jednicce.

rughar · 31. 07. 2008 14:16

↑ Pavel:

Já napsal dvě podmínky, kde musí být splněna jedna z nich. Tys napsal jenom jednu z těch dvou a řekl jsi, že musí být splněna. Tedy jsi trochu ubral na obecnosti. Ale to nemá moc smysl řešit, protože v tom příkladu to nehraje roli. A naopak podmínku, co jsi sám napsal tak nesplňuješ (tohle popravdě jenom hádám, ale z toho posledního grafu je do opravdu hodně patrné). Ale pravděpodobně jsem jenom zmatený. Je řeč o té úplně první limitě nebo o té poslední???

Lishaak · 31. 07. 2008 15:31

↑↑ rughar:

Tohle me zaujalo. Opravdu existuje deterministicky algoritmus, ktery vyresi kazdou limitu? Co to presne znamena kazdou? Kazdou limitu posloupnosti nebo i funkce? A jake funkce? Kazde, jejiz predpis lze zapsat pomoci elementarnich funkci?

Jo a jeste jedna vec, neni me jasne jak s tematem souvisi kleinova lahev...

Marian · 31. 07. 2008 15:42 — Editoval Marian (31. 07. 2008 15:43)

↑ Lishaak a rughar:

Je to - dle meho - nesmysl. Neni vubec jasne, co to znamena vyresit nejakou limitu. Vemme si treba limitu
$\lim_{n\to\infty}\sum_{j=1}^n\frac{1}{j^3}.$

Vime, ze limita existuje, R. Apéry dokazal dokonce, ze se jedna o iracionalni cislo, ale neumime najit jeji hodnotu pomoci konecneho poctu elementarnich funkci. Proto pretrvava od dob Riemanna oznaceni $\zeta (3)$ .

Tedy nejsem si jisty, o jaky deterministicky algoritmus se jedna. Uvedl jsem jen jeden a hodne specificky priklad. Jinych prikladu bych mohl uvest nespocetne.

rughar · 31. 07. 2008 16:20 — Editoval rughar (31. 07. 2008 16:25)

↑ Lishaak:

Měl jsem na mysli takové limity, které jsou zadány složením spojitých a diferencovatelných funkcí. V případě limity

$\lim\limits_{n \to \infty}n((1+\frac{1}{n})^n-e)$

si ji mohu rozložit na funkce

$(1-\frac{1}{n})^n$
$n$

Nyní provedu Taylorův rozvoj. Bude stačit do prvního řádu. T. rozvoj první funkce (jako parametr si zolím q = 1/n)

$T((1-q)^\frac{1}{q})(0)=e-\frac{e}{2}q+o(q)^2$
$T((1-\frac{1}{n})^n)(\infty)=e-\frac{e}{2}\frac{1}{n}+o(\frac{1}{n})^2$

(Nechápu, proč to tam u prvního řádku zobrazuje 1q, když to mělo zobrazit 1/q a chybu tam ne a na najít :-()

Rozvoj té funkce můžeme dosadit za danou funkci v limitě. Zůstane tedy

$\lim\limits_{n \to \infty}n(e-\frac{e}{2n}-e)$

Což je jednoduše -e/2

Čím je Taylorův rozvoj problémový je to, že se tam musí hodně derivovat a po každé derivaci se musí spočítat další limita. Popsal bych to tedy shrnutě takovýmto způsobem:

Máme limitu

$\lim\limits_{n \to n_0}f(n)$

1. "rozložit" si funkci f na takové funkce, které umím derivovat a u kterých dokážu spočítat limitu n -> n0.
2. Spočítat Taylorův rozvoj jednotlivých funkcí (většinou stačí do již prvního řádu) kolem bodu n0.
3. Dosadit Taylorovi rozvoje jednotlivých funkcí za dané funkce
4. Dopočítáme tak, že prostě dosadíme :-)

Po kroku 4 bychom se měli dopracovat, že budeme počítat limitu podílu polynomů (a nikdy jinak), což je již triviální záležitost.

↑ Marian:

Uznávám, že na posloupnosti to nefunguje (to by bylo opravdu hezké mít kanón na to jak sečíst každou řadu :-)). Funguje to pouze na funkce.

Marian · 31. 07. 2008 17:00 — Editoval Marian (31. 07. 2008 17:01)

↑ rughar:

Chces-li v exponentu zlomek, je potreba exponent umistit do slozenych zavorek {} za znak ^. Chybi ti tam prave ty slozene zavorky.

Nefunguje to ani pro funkce. Vemu funkci

$\zeta (x):=\sum_{j=1}^{\infty}\frac{1}{j^x} .$

Ze se jedna o funkci, je jasne - nazyva se Riemnnova funkce 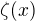$\zeta (x)$ . Ukaz mi ted, jak je mozne spocitat treba

$\lim_{x\to 2}\zeta (x)=\frac{\pi ^2}{6}.$

Musis si uvedomit, ze mnohe funkce jsou jiz definovany jako nekonecna rada nebo podobnym a nekdy jedinym moznym zvrhlym (relativni ...) zpusobem. Myslim, ze ti to neprojde ani pro funkce, ktere jsou dany nejak rozumne, ale mohu se mylit. Mam zrovna jinou praci, takze na kontrapriměr nemam cas.

rughar · 31. 07. 2008 17:12

↑ Marian:

"... takové limity, které jsou zadány složením spojitých a diferencovatelných funkcí."

... jsem, uvedl ve svém příspěvku. Možná jsem ještě k tomu mohl připsat konečným. Nebo? pokud zadáš funkci tak, že ji vyjádříš jako součet nekonečně mnoha funkcí, tak už ani není zakopený pes v limitě jako spíš v tom, že nedokážeš sečíst tu řadu. A tím pádem nedokážeš funkci rozložit na takové, u kterých můžeš udělat Taylorův rozvoj.

Za použití čistě elementárních funkcí (konečeného počtu) Taylorův rozvoj vždy vyhraje. Protože umí tyto funkce převést na polynomy. A limitu, která se skládá z (konečného počtu) polynomů umíme počítat vždy.

Marian · 31. 07. 2008 17:31

↑ rughar:

O.K.

Pavel Brožek

↑ rughar:

O substituci jsem se zmínil, aby byl srozumitelný ten graf, kde je znázorněna závislost na proměnné x. To, že na grafu funkce "osciluje", je zřejmě způsobeno výpočtem funkčních hodnot v Mathematice, čím blíž jsme nule, s tím extrémně menšími/většími čísly se pracuje a dochází k zanesení chyby do výsledku. Lze ukázat, že i v okolí nuly je funkce monotónní.

Pavel uvedl pouze jednu z podmínek pro větu o limitě složené funkce, protože ta zde stačí - vnitřní funkce $x=\frac1n$ nikde na redukovaném okolí $+\infty$ nenabývá své limity 0. Druhá podmínka, která pokud je splněna pak věta také platí, je, že vnější funkce je spojitá v bodě, kde počítáme její limitu (tahle podmínka tu splněna není).

EDIT: A ještě co se týče možnosti komplexního výsledku - první limita v příspěvku #48 je kladná, tzn., že existuje $n_0$ takové, že pro všechny $n>n_0$ je posloupnost kladná. Výraz umocňovaný v druhé limitě je tedy pro velké n kladný a kladné číslo na kladné má imaginární složku vždy nulovou. Komplexní číslo jako výsledek tedy nepřipadá v úvahu.

Pavel · 31. 07. 2008 22:04 — Editoval Pavel (31. 07. 2008 22:08)

Pokud jde o tu poslední limitu, vyšlo mi

$\lim_{n\to\infty}\left(\frac{n\left(\Biggl(\frac {n(\bigl(1+\frac 1n\bigr)^n-e)}{-\frac e2}\Biggr)^n-e^{-\frac{11}{12}}\right)}{\frac{131}{288}e^{-\frac{11}{12}}}\right)^n=\,\dots\,=e^{-\frac{55537}{125760}}\,.$

Dál bych už opravdu nešel :-)

↑ Marian:

Z Kleinovy láhve se bude pít dost blbě :-) Jen pro zajímavost, skutečnou Kleinovou láhev jsem našel tady:

http://www.youtube.com/watch?v=Ra62LW6NuGk

Pavel Brožek

↑ Pavel:

Mohl bys prosím přiblížit postup, jak ses k tomu výsledku dostal? Odpovídá to odhadu z grafu, ale nenapadá mě jak ověřit, že to je správně. Vždy? to je tak hrozná limita, snad jsi ji nepočítal na papíře :-)

EDIT: Už se mi podařilo dostat se k témuž výsledku přes Mathematicu - rozvíjel jsem postupně do řad, najednou to nezvládá.

Pavel · 01. 08. 2008 00:45

Počítal :-) Šel jsem na to hrubou silou. Co se dalo, nahradil jsem Taylorem. Začal jsem rozvojem do $\small o(x^5)$ a pak už to šlo nějak samo.

Limitu jsem nejdříve upravil:

$\lim_{n\to\infty}\left(\frac{n\left(\Biggl(\frac {n(\bigl(1+\frac 1n\bigr)^n-e)}{-\frac e2}\Biggr)^n-e^{-\frac{11}{12}}\right)}{\frac{131}{288}e^{-\frac{11}{12}}}\right)^n= \lim_{x\to 0^+}\left(\frac{\Biggl(\frac {\bigl(1+x\bigr)^{\frac 1x}-e}{-\frac e2x}\Biggr)^{\frac 1x}-e^{-\frac{11}{12}}}{x\frac{131}{288}e^{-\frac{11}{12}}}\right)^{\frac 1x}$

Začal jsem rozvojem $(1+x)^{\frac 1x}-e$ tak, jak si ho použil v některém z předchozích příspěvků

$(1+x)^{\frac 1x}-e=e(e^{\frac 1x\ln(x+1)-1}-1)=e(e^{\frac 1x(x-\frac {x^2}2+\frac{x^3}3-\frac{x^4}4+\frac{x^5}5+o(x^5))-1}-1)=e(e^{-\frac {x}2+\frac{x^2}3-\frac{x^3}4+\frac{x^4}5+o(x^4)}-1)=\nl =e\biggl(1+(-\frac {x}2+\frac{x^2}3-\frac{x^3}4+\frac{x^4}5+o(x^4))+\frac 12(-\frac {x}2+\frac{x^2}3-\frac{x^3}4+\frac{x^4}5+o(x^4))^2+\frac 16(-\frac {x}2+\frac{x^2}3-\frac{x^3}4+\frac{x^4}5+o(x^4))^3+\frac 1{24}(-\frac {x}2+\frac{x^2}3-\frac{x^3}4+\frac{x^4}5+o(x^4))^4+o(x^4)-1\biggr)=\,\dots\nl \dots\,=e\biggl(-\frac x2+\frac{11}{24}x^2-\frac{21}{48}x^3+\frac{2447}{5760}x^4\biggr)+o(x^4)$

$\frac{(1+x)^{\frac 1x}-e}{-\frac e2x}=1-\frac{11}{12}x+\frac{21}{24}x^2-\frac{2447}{2880}x^3+o(x^3)$

$\biggl(\frac{(1+x)^{\frac 1x}-e}{-\frac e2x}\biggr)^{\frac 1x}=e^{\frac 1x\ln(1-\frac{11}{12}x+\frac{21}{24}x^2-\frac{2447}{2880}x^3+o(x^3))}=e^{\frac 1x(-\frac{11}{12}x+\frac{21}{24}x^2-\frac{2447}{2880}x^3+o(x^3)-\frac 12\bigl(-\frac{11}{12}x+\frac{21}{24}x^2-\frac{2447}{2880}x^3+o(x^3)\bigr)^2+\frac 13\bigl(-\frac{11}{12}x+\frac{21}{24}x^2-\frac{2447}{2880}x^3+o(x^3)\bigr)^3+o(x^3))}=\,\dots\nl \dots\,=e^{-\frac{11}{12}+\frac{131}{288}x-\frac{493}{1620}x^2+o(x^2)}$

$\biggl(\frac{(1+x)^{\frac 1x}-e}{-\frac e2x}\biggr)^{\frac 1x}-e^{-\frac{11}{12}}=e^{-\frac{11}{12}}(e^{\frac{131}{288}x-\frac{493}{1620}x^2+ o(x^2)}-1) =e^{-\frac{11}{12}}(1+\frac{131}{288}x-\frac{493}{1620}x^2+ o(x^2)+\frac 12\bigl(\frac{131}{288}x-\frac{493}{1620}x^2+ o(x^2)\bigr)^2+o(x^2)-1)=\,\dots\nl \dots\,=e^{-\frac{11}{12}}(1+\frac{131}{288}x-\frac{166611}{829440}x^2)+o(x^2)$

$\frac{\biggl(\frac{(1+x)^{\frac 1x}-e}{-\frac e2x}\biggr)^{\frac 1x}-e^{-\frac{11}{12}}}{x\frac{131}{288}e^{-\frac{11}{12}}}=1-\frac{55537}{125760}x+o(x)$

$\left(\frac{\biggl(\frac{(1+x)^{\frac 1x}-e}{-\frac e2x}\biggr)^{\frac 1x}-e^{-\frac{11}{12}}}{x\frac{131}{288}e^{-\frac{11}{12}}}\right)^{\frac 1x}=e^{\frac 1x\ln(1-\frac{55537}{125760}x+o(x))}=e^{\frac 1x(-\frac{55537}{125760}x+o(x))}=e^{-\frac{55537}{125760}+o(1)}$

Pavel Brožek

Nakonec to nevypadá tak špatně, stačí udělat pár rozvojů a máš limitu :-) Nenapadá mě ale způsob, jakým by se z tohohle postupu dalo odvodit pravidlo jak by vypadaly další limity. To už bych ale neřešil :-)

Matematické Fórum

#51 31. 07. 2008 10:51 — Editoval BrozekP (31. 07. 2008 10:51)

Re: Prázdninová limita

#52 31. 07. 2008 12:35

Re: Prázdninová limita

#53 31. 07. 2008 12:36

Re: Prázdninová limita

#54 31. 07. 2008 13:03 — Editoval rughar (31. 07. 2008 13:05)

Re: Prázdninová limita

#55 31. 07. 2008 13:33 — Editoval Marian (31. 07. 2008 13:36)

Re: Prázdninová limita

#56 31. 07. 2008 13:41

Re: Prázdninová limita

#57 31. 07. 2008 13:45

Re: Prázdninová limita

#58 31. 07. 2008 13:46 — Editoval Marian (31. 07. 2008 13:47)

Re: Prázdninová limita

#59 31. 07. 2008 14:16

Re: Prázdninová limita

#60 31. 07. 2008 15:31

Re: Prázdninová limita

#61 31. 07. 2008 15:42 — Editoval Marian (31. 07. 2008 15:43)

Re: Prázdninová limita

#62 31. 07. 2008 16:20 — Editoval rughar (31. 07. 2008 16:25)

Re: Prázdninová limita

#63 31. 07. 2008 17:00 — Editoval Marian (31. 07. 2008 17:01)

Re: Prázdninová limita

#64 31. 07. 2008 17:12

Re: Prázdninová limita

#65 31. 07. 2008 17:31

Re: Prázdninová limita

#66 31. 07. 2008 17:37 — Editoval BrozekP (31. 07. 2008 17:59)

Re: Prázdninová limita

#67 31. 07. 2008 22:04 — Editoval Pavel (31. 07. 2008 22:08)

Re: Prázdninová limita

#68 31. 07. 2008 23:37 — Editoval BrozekP (01. 08. 2008 00:16)

Re: Prázdninová limita

#69 01. 08. 2008 00:45

Re: Prázdninová limita

#70 01. 08. 2008 11:30 — Editoval BrozekP (01. 08. 2008 11:30)

Re: Prázdninová limita

Zápatí