Matematické Fórum

luckym · 15. 11. 2011 09:40 — Editoval luckym (15. 11. 2011 09:46)

Ahojte pokracujem z tohota vlakna: http://forum.matweb.cz/viewtopic.php?id=36498#p232400

Takze to skusim este raz vysvetlit:
vedeli by ste prosim poradit ci existuje nejaky SW (derive som skusal tam sa mi to nedalo...(alebo neviem) stacilo by mi nazov sw nech neskusam vsetko) ktory by dokazal symbolicky vyjadrit tento integral:
$\int_{K}f(x,y)$ je to integral na oblasti K, v mojom pripade trojuholnik dany suradnicami bodov A,B,C. v rovine, cize mam body: $[x_1, y_1] [x_2, y_2] [x_3, y_3]$ to su konstanty

Rucne to spravit viem (transformujem to na trojuholnik[0 0] [0 1] [1 0] a potom zinegrujem v medziach [0 1] a [0 1-u]) ale ta fcia je trocha komplikovanejsia a potrebujem to spravit pre viac takychto funkcii.
ta fcia je napr. nieco taketo: $f(x,y) = x^2 - 2x_1x +x_1^2 + y^2 - 2 y_1 y + y_1^2$

takze ked by som to zintegroval dostanem 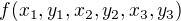$f(x_1, y_1,x_2,y_2,x_3, y_3)$ -> toto je to co potrebujem dostat z toho SW

dik.

kaja.marik · 15. 11. 2011 10:08

Asi bude potreba si naprogramovat proceduru, ktera dela presne to, co popisujete.
V derive se moc programovat neda, takze snad nejaky vyspelejsi CAS.

Maxima, Maple i Mathematica by to mely zvladnout, ale kazdy ma svuj programovaci jazyk a je potreba se jej ucit. Ale neni to nic tezkeho.

Mozna Sage, tam se programuje v Pythonu.

luckym · 16. 11. 2011 22:16

↑ kaja.marik:

ok dakujem, aj to staci... takze ten postup programovat.... asi to nejak skombinujem..:)

Matematické Fórum

#1 15. 11. 2011 09:40 — Editoval luckym (15. 11. 2011 09:46)

integral na oblasti -> symbolicke riesenie

#2 15. 11. 2011 10:08

Re: integral na oblasti -> symbolicke riesenie

#3 16. 11. 2011 22:16

Re: integral na oblasti -> symbolicke riesenie