Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Exponenciála tenzoru (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 11. 2011 17:40
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Exponenciála tenzoru
Ahoj, mám dokázat, že pro komutativní tenzory  ,
,  platí:
platí: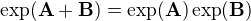 ,
,
kde  značí skládání tenzorů (
značí skládání tenzorů (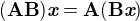 ,
,  ).
).
Kam jsem se dostal:![kopírovat do textarea $\exp(\mathbf A + \mathbf B)=\sum_{k=0}^{\infty}\frac{(\mathbf A + \mathbf B)^k}{k!}=\sum_{k=0}^{\infty}\[ \frac{1}{k!}\sum_{i=0}^{k} {k\choose i}\mathbf{A}^i\mathbf{B}^{k-i} \]=\sum_{k=0}^{\infty}\[ \sum_{i=0}^{k} \frac{k!}{(k-i)!i!k!}\mathbf{A}^i\mathbf{B}^{k-i} \]=\sum_{k=0}^{\infty}\[ \sum_{i=0}^{k} \frac{\mathbf{A}^i\mathbf{B}^{k-i} }{(k-i)!i!}\]$](/mathtex/3d/3d010a2aaced3e30bb5344c377c34790.gif)
 .
.
Výrazy už vypadají podobně, ale neumím to dokončit. Díky za rady!
Offline
- (téma jako vyřešené označil(a) FliegenderZirkus)
#3 16. 11. 2011 21:01
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Exponenciála tenzoru
↑ Stýv:
Obrázek nakonec pomohl a dál už je to jasné. Dík, vyřešeno
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Exponenciála tenzoru (TOTO TÉMA JE VYŘEŠENÉ)
 (doporučuju nakreslit si obrázek) a pak posun indexu
(doporučuju nakreslit si obrázek) a pak posun indexu