Matematické Fórum

Sulfan · 18. 11. 2011 19:55

Ahoj, řeším následující limitu posloupnosti:
$\lim n\cdot \left ( \sqrt[n]{e}-1 \right )$

Rozšíření dle vzorce $a^n-b^n$ příliš nepomohlo a tak jsem úvahou zjistil, že by se dala Heineovou větou převést na limitu funkce a potom udělat nějaká substituce (například $\frac{1}{x}$ v $\frac{e^{1/x}-1}{\frac{1}{x}}$ ), ale rád bych to řešil jako limitu posloupnosti (a ne jako funkce), nevíte někdo jakou úpravu provést?

Děkuji.

jelena · 19. 11. 2011 17:19

Zdravím,

není to můj výmysl - je z "AntiDemidoviče" - "Ляшко, Боярчук, Гай, Головач Математический анализ, том 1". Doporučuji vycházet z nerovnosti:

$$1+\frac{1}{n}$^n<e<$1+\frac{1}{n-1}$^n$

Účel příspěvku - Tvé téma nějak zapadlo, snad si ho někdo z kolegu všimne. Děkuji.

moto_moto · 19. 11. 2011 17:41

Dobry den,
mam ulohu:
$\lim_{x\to\infty}\frac{(x+1)^{10}+(x+2)^{10}+...+(x+100)^{10}}{x^{10}+10^{10}}$

citatel jsem prevedl na "sumu":

$\sum_{i=1}^{100}(x+i)^{10} = \sum_{i=1+x}^{100+x}i^{10}$

potreboval bych vedet jak vypocitam soucet vsech clenu rady.
Predem dekuji za odpoved

jelena · 19. 11. 2011 17:49

↑ moto_moto:

Zdravím,

vytkla bych dominantního člena 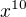$x^{10}$ v čitateli a v jmenovateli (v závorkách zůstane 1 + "nějaké drobné" - představím si, jak vypadá binomický rozvoj).

Na 1. příspěvek - velmi pěkný zápis a formulace problému, jen poprosím příště zakládat si vlastní téma, tedy pokud budeš potřebovat pokračovat, založ si prosím vlastní téma, děkuji.

moto_moto · 19. 11. 2011 17:54

↑ jelena:
ok, dekuji

FailED · 20. 11. 2011 13:00 — Editoval FailED (20. 11. 2011 13:16)

Zdravím,

reaguji na příspěvek ↑ sulfan::

Jak píše ↑ Jelena:, stačí využít věty o dvou policajtech s použitím těch nerovností, kde ses zasekl?

$\lim n$\frac{n+1}{n} -1$\le \lim n$\sqrt[n]{e}-1$ \le \lim n$\frac{n}{n-1}-1$$

Sulfan · 20. 11. 2011 13:08

↑ FailED: Teď už je to jasné, díky. Zasekl jsem se na tom, že jsem nedokázal odhadnout $\sqrt[n]{e}$ pomocí lineární lomené funkce (která vypadla při odmocnění příspěvku od ↑ Jelena:).

Označuji jako vyřešeno.

Matematické Fórum

#1 18. 11. 2011 19:55

Limita posloupnosti

#2 19. 11. 2011 17:19

Re: Limita posloupnosti

#3 19. 11. 2011 17:41

Re: Limita posloupnosti

#4 19. 11. 2011 17:49

Re: Limita posloupnosti

#5 19. 11. 2011 17:54

Re: Limita posloupnosti

#6 20. 11. 2011 13:00 — Editoval FailED (20. 11. 2011 13:16)

Re: Limita posloupnosti

#7 20. 11. 2011 13:08

Re: Limita posloupnosti

Zápatí