Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 25. 11. 2011 23:17

Sulfan
Příspěvky: 373
Reputace:   23 
 

Limita posloupnosti

Ahoj,
řeším limitu posloupnosti 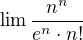$\lim \frac{n^{n}}{e^{n}\cdot n!}$, zatím se mi podařilo dokázat, že
(1) posloupnost je ostře klesající
(2) má reálnou limitu L, kde 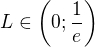$L \in \left ( 0;\frac{1}{e} \right )$

Zkoušel jsem příklad odhadovat nebo zkoušet určovat infimum množiny všech prvků posloupnosti, to je ale slepá ulička. Jak limitu vypočítat?

Offline

  • (téma jako vyřešené označil(a) Sulfan)

#2 25. 11. 2011 23:46 — Editoval OiBobik (25. 11. 2011 23:50)

OiBobik
Moderátor
Místo: Brno/Praha
Příspěvky: 1013
Škola: MFF UK Mat. struktury
Pozice: student
Reputace:   82 
 

Re: Limita posloupnosti

↑ Sulfan:

Ahoj, tady se bude hodit Stirlingova formule, odhadující faktoriál (resp. příklad vypadá na Stirlinga jak dělaný : )) ).

"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]

Offline

 

#3 26. 11. 2011 10:29

Sulfan
Příspěvky: 373
Reputace:   23 
 

Re: Limita posloupnosti

↑ OiBobik: To je pěkná aproximace, dosud jsem o ní nevěděl. Zřejmě to bude asi nejméně náročný způsob jak limitu spočítat. Díky.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson