Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 21. 10. 2007 20:39
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Posloupnost
zkus si napsat prvních pár hodnot a uvidíš, jestli a) platí nebo ne.
b)pokud už jste probírali L'Hospitalovo pravidlo, tady ho lze využít.
c)do takového grafu stačí vyznačit prvních pár hodnot a pak se to chová podobně jako exponenciální funkce...
d)řešíme rovnici 2^n/4n=2048/7. Protože zlomek napravo vznikl krácením zlomku nalevo, musí být 4n dělitelné 7, takže musí být n dělitelné 7. Navíc musí být čitatel nezkráceného zlomku alespň 2048=2^11, proto n>11. Nejmenší možné n je proto 14. Ověříme , že vyhoví.
Pozn.Protože je od indexu 3 posloupnost rostoucí, je toto n jediné vyhovující, ale na to se nás nikdo neptá.
e) vzhledem k tomu, že v b) nám vyšla limita nekonečno, tak omezená není.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 21. 10. 2007 21:55 — Editoval andrew (21. 10. 2007 22:02)
Re: Posloupnost
to Kondr
zkus si napsat prvních pár hodnot a uvidíš, jestli a) platí nebo ne.
To je zasadni chyba jez by se nemela vubec ve cvicenich ci prednaskach vyskytovat. Co treba posloupnost 
Ta je pro prvnich par hodnot rostouci. Takze lze odtud usuzovat, ze tato posloupnost je rostouci pro vsechna  ? Nikoliv, toto se resi nasledovne:
? Nikoliv, toto se resi nasledovne:
Napriklad se muzeme zeptat, plati  pro vsechna
pro vsechna  ?
?
Tohle kdyz vyresime, dospejeme k  a odtud mohu tvrdit, ze posloupnost
a odtud mohu tvrdit, ze posloupnost  je rostouci pro
je rostouci pro  a klesajici pro vsechna
a klesajici pro vsechna  .
.
b)pokud už jste probírali L'Hospitalovo pravidlo, tady ho lze využít.
Opet velika chyba. Rec je o posloupnostech a ne o funkcich. Jak byste chtel derivovat posloupnost?
Toto se resi tak, ze si rekneme 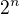 roste daleko rychleji nez
roste daleko rychleji nez  a proto
a proto  .
.
Pro doplneni, obdobu L'Hospitalova pravidla u posloupnosti je tzv, Stolzova veta.
Offline
#4 21. 10. 2007 22:13
Re: Posloupnost
to andrew
přestože mi vyšetřování průběhu posloupnosti podle prvních pár členů přijde také podezřelé, rozhodně bych svůj argument nepodal takto drsným způsobem. Škoda, že už se tu na fóru nezobrazují počty příspěvků jednotlivých uživatelů. Bylo by ihned vidět, že Kondr není z těch, kdo by potřeboval takováto kázání.
Taky mi přijde divné, že člověk, který je takto obeznámen se Stolzovou větou (což už je podle mého jeden z pokročilejších poznatků) není obeznámen s větou Heineho (což je poznatek základní), která ospravdlňuje použití L'Hospitalova pravidla u posloupností....
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#5 21. 10. 2007 22:51 — Editoval andrew (21. 10. 2007 22:52)
Re: Posloupnost
to Lishaak
Ehh, co je na mem predchozim prispevku drsneho? :)
Škoda, že už se tu na fóru nezobrazují počty příspěvků jednotlivých uživatelů. Bylo by ihned vidět, že Kondr není z těch, kdo by potřeboval takováto kázání.
Mam to chapat tak, ze id Kondr je znacne vytizen (buh vi jak) a ze nemel cas radne odpovedet? Protoze pak nechapu souvislost s pocty prispevku a kazanim...
A jestli to vyznelo jako kazani, tak se omlouvam, ale matematika se neda delat jinak nez presne a precizne.
... není obeznámen s větou Heineho ...
S vetou Heineho jsem obeznamen nebyl, ale s definici ano. A jak jsem na netu a ve skriptech nasel, imho jedno jsou. Takze zalezi na dotycnem autorovi zda se rozhodne to napsat jako definici ci vetu. A v cem presne tato Heineho veta (resp. def.) ospravedlnuje pouziti l'Hospitalovo pravidlo? Ja to v tom nevidim... :(
Offline
#6 21. 10. 2007 23:17
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Posloupnost
andrew napsal(a):
to Kondr
zkus si napsat prvních pár hodnot a uvidíš, jestli a) platí nebo ne.
To je zasadni chyba jez by se nemela vubec ve cvicenich ci prednaskach vyskytovat.
Já si třeba myslím, že v tomto konkrétním příkladě je to nejrychlejší cesta k vítězství. Vypočítám si první dva členy posloupnosti -- 1/2, 1/2 -- a odpověď na otázku je jasná, není ostře klesající ani ostře rostoucí.
2+2=4
Offline
#8 21. 10. 2007 23:32
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Posloupnost
@Lishaak: i Kondr občas potřebuje kázání, ale díky za zastání
@Lukee: přesně tohle jsem chtěl napsat -- prohlížení prvních prvků je dobré na hledání protipříkladů, ne na hledání důkazů. Doporučuju ho provést před tím, než začneme dokazovat, že nějaká nerovnost platí.
@andrew: díky za připomínky. Btw. nezkušený matematik by neměl používat pojem "mnohem rychleji" ;)
Zapojil bych se do diskuse dřív, ale snažil jsem se dokázat korektnost použití toho L'Hospitala.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#9 21. 10. 2007 23:33
- Lukee

- Administrátor

- Místo: Opava
- Příspěvky: 1863
- Škola: UPOL, Informatika
- Pozice: Roznašeč reklamních bannerů
- Web
Re: Posloupnost
@andrew: On bude asi problém v této Kondrově větě, že? „zkus si napsat prvních pár hodnot a uvidíš, jestli a) platí nebo ne.” Z této věty lze vyvodit, že by tento postup šel použít obecně, resp. že by dosazování mohlo být bráno jako důkazní břemeno, ale nemyslím si, že by to Kondr takto myslel, ač tedy nechci mluvit za něj :-). Lépe by ta věta měla znít „zkus si napsat prvních pár hodnot a uvidíš, že a) neplatí.”. Pak už by to tedy bylo jednoznačnější.
Edit: Á Kondr už stihl odpovědět :-). Nevadí, své věty zde již ponechám.
2+2=4
Offline
#12 21. 10. 2007 23:49 — Editoval Kondr (22. 10. 2007 09:10)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Posloupnost
Zkusme tento trik:
počítáme lim a_n/b_n.
najdeme fce takové, že
a_n=f(1/n),
b_n=g(1/n),
f a g jsou spojité na (0,oo)
Pak 

(platí vzhledem ke spojitosti f a g)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#14 22. 10. 2007 15:53 — Editoval andrew (22. 10. 2007 15:55)
Re: Posloupnost
to Kondr
Porad nejak nerozumim Vasemu predchozimu prispevku. :( Proc jsou funkce  a
a  spojite? A jak spolu souvisi
spojite? A jak spolu souvisi  a
a  v tech limitach?
v tech limitach?
to leniczcha
To se resi "metodou puleni intervalu". Pro jednoduchost si prepiseme 
Nyni si zvolime napriklad  a vypocteme
a vypocteme  . Odtud vidime, ze jsme prestrelili
. Odtud vidime, ze jsme prestrelili  a proto zvolime
a proto zvolime  mensi. Napr.
mensi. Napr.  , spocteme
, spocteme  , coz je zase moc malo. Takze zkusime
, coz je zase moc malo. Takze zkusime  , opet stanovime
, opet stanovime  . A hle, tot je nas hledany index
. A hle, tot je nas hledany index  , tj. hledany index je
, tj. hledany index je 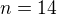 .
.
Offline
#16 22. 10. 2007 17:55
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Posloupnost
@andrew: tak já to zkusím ještě přeformulovat. Oproti předchozímu příspěvku změním význam funkcí f a g,
protože ty úpravy s převrácenou hodnotou byly zbytečné:
Nech? f(x) a g(x) jsou funkce  , které mají ve všech bodech derivaci a navíc f(x)/g(x) a f'(x)/g'(x) mají limity L_1, L_2 pro x->oo. Z L'Hospitalova pravidla L1=L2.
, které mají ve všech bodech derivaci a navíc f(x)/g(x) a f'(x)/g'(x) mají limity L_1, L_2 pro x->oo. Z L'Hospitalova pravidla L1=L2.
Nech? a_n, b_n, c_n, d_n jsou posloupnosti taové, že a_n=f(n), b_n=g(n), c_n=f'(n), d_n=g'(n).
Pak lim(a_n/b_n)=L_1=L_2=lim(c_n/d_n).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#18 22. 10. 2007 20:51
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Posloupnost
posloupnosti derivovat nepotřebuju... jen využii faktu, že liimita posloupnosti a/b se rovná limitě funkce f/g, ta se podle L'Hospitala rovná limitě f'/g' a ta se rovná limitě posloupnosti c/d. Funguje to jenom pokud funkce f,g existují a mají určité vlastnosti (viz výše), ale chybu v tom postupu nevidím.
Jinak nejsem sám, kdo by to takto počítal ;) http://math.feld.cvut.cz/mt/txta/2/txc3ab2e.htm
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#19 22. 10. 2007 23:25 — Editoval andrew (22. 10. 2007 23:58)
Re: Posloupnost
to Kondr
posloupnosti derivovat nepotřebuju...
Tak co je potom c_n=f'(n), d_n=g'(n)?
Vami odkazovany web nevypada moc verohodne. Vubec nikde jsem nenasel kdo je autorem ci kdy byla provedena posledni aktualizace stranek apod. veci. Projdete-li si par stranek naleznete takove perly jako "... jak f tak g mají v nekonečnu nekonečnou limitu..." Co je probuh nekonecna limita? Dale "... když už nemůžeme spočítat odpověď, ..". Co to je "spocitat odpoved"? A to jsem jenom namatkou prosel par stranek. Z takovehoto webu doporucuji neziskavat informace a natoz jim pak verit.
Napr. na http://math.feld.cvut.cz/mt/txta/2/txc3aa2e.htm
je veta jejiz jednu cast sem vypichnu. Uz to, ze posl. a_n se definuji jako zobrazeni prirozenych cisel (ne celych cisel) do R zavani autorovo neznalosti def. posl. nebo je to jeho nepozornost? To vazne nevim... .
Nech? f(x) je funkce definovaná na nějakém intervalu (K,oo), definujme posloupnost a_n=f(n) pro celá čísla n>K.
Jestliže je f monotonní, pak je i posloupnost {a_n} monotonní (ve stejném směru).
Coz neni pravda. Zvolme interval (0, oo) a funkci  , ta je ostre rostouci na prislusnych intervalech. Pak podle te vety plyne, ze posloupnost
, ta je ostre rostouci na prislusnych intervalech. Pak podle te vety plyne, ze posloupnost  je ostre rostouci. Coz je spor.
je ostre rostouci. Coz je spor.
Offline
#20 23. 10. 2007 00:16
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Posloupnost
Nejprve k dotazu:
rovnost c_n=f'(n)
říká, že c_n je je posloupnost fukčních hodnot funkce f' v bodech 1,2,3,... kde funkce f' je derivace funkce f. Pojem derivace posloupnosti zavádět nepotřebuji.
Co se týče definice posloupnosti je zřejmě nutno o neznalosti a nepozornosti mluvit i v souvislosti s autory (a potažmo i čtenáři) anglické Wikipedie... http://en.wikipedia.org/wiki/Sequence
A co se týče platnosti či neplatnosti zmiňované věty, pak bych upozornil na to, že
funkce  není rostoucí a nelze ji tudíž použít jako protipříklad.
není rostoucí a nelze ji tudíž použít jako protipříklad.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#21 23. 10. 2007 08:08 — Editoval Marian (23. 10. 2007 08:10)
Re: Posloupnost
Zdravim vsechny zucastnene.
Nebudu se nyni vyjadrovat, kdo z vas dvou (Kondr nebo andrew) ma pravdy vice, protoze na to ted nemam cas, ale pridam jedno misto na zminovanem webu, ktere zaslouzi kritiku. Totiz autor definuje "posloupnost" a_n=... . O par radku nize pak hovori o posloupnosti {a_n}. Problem je urcite jasny. Definovanim obecneho clene posloupnosti nemuzeme jeste, by? formalne, o posloupnost hovorit. Dale diskutovana veta ma mnoho nejasnych terminu
* na nějakém intervalu (K,oo),
* omezena v nejakem smyslu,
* monotonni ve stejnem smyslu,
* etc.
Offline
#23 10. 12. 2008 18:35
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Posloupnost
Omlouvam se ze vyhrabavam tuto debatu, ale pro pripadne budouci ctenare tohoto vlakna: ctu clanek o diferencnich rovnicich, kde se pouziva "diskretni l'Hospitalovo pravidlo" a autori se odkazuji na knihu Ravi P. Agarwal - Difference equations and indequalities, Marcel Dekker (2000).
Tak tam pripadni zajemci o tuto problematiku asi najdou detailnejsi pouceni.
Offline