Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 03. 12. 2011 15:25 — Editoval Andrejka3 (04. 12. 2011 13:29)
Re: Lienární algebra - Binární operace (2)
Edit: omlouvám se, psala jsem, když nebyla odpověď
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 03. 12. 2011 15:46
Re: Lienární algebra - Binární operace (2)
↑ Andrejka3:
Tvoje vysvětlení je lepší. Než bych já ze sebe něco takového vysoukal, tak by se vrátila Haleyova kometa;)
Offline
#6 03. 12. 2011 22:25
Re: Lienární algebra - Binární operace (2)
↑ lamnik:
Ne.
Úroveň 1: body čtverce
Úroveň 2: operace symetrie - zobrazení množiny  na sebe samu.
na sebe samu.
Úroveň 3: skládání operací symetrie (binární operace mezi prvky z 2. úrovně)
Otáčení podle os stran je operace symetrie, tedy prvek 2. úrovně, stejně jako rotace.
Otáčení podle uhlopříček rovněž. Spíš bych to ale nazvala zrcadlení.
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 04. 12. 2011 11:49
Re: Lienární algebra - Binární operace (2)
Vypiš všechny symetrie. Napiš přesně co dělají.
Je skládání operací symetrie asociativní? Proč?
Zkoumej, co se děje, když složíš rotaci s rotací. Je skládání rotací komutativní?
Co je výsledkem složení rotací a zrcadlení? Je to komutativní?
Je skládání zrcadlení se zrcadlením komutativní? Vznikne zrcadlení nebo rotace?
Vždyť to je zajímavá hra.
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 04. 12. 2011 11:56 — Editoval Andrejka3 (04. 12. 2011 11:56)
Re: Lienární algebra - Binární operace (2)
Ctverec
D C
A B
Rotace:
1) Identita 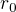 .
.
Vysledek operace:
D C
A B
Zobrazuje tedy (horni radek jsou vzory, dolni prislusne obrazy)
A B C D
A B C D
2) rotace o 90 st. 
Vysledek operace
C B
D A
Tabulka:
A B C D
D A B C
3) rotace o 180 
Vysledek operace
B A
C D
Tabulka:
A B C D
C D A B
Pozorovani: Kdyz ctu pismenka v kladnem smeru, zachova se poradi.
Pokracuj.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 04. 12. 2011 12:30
Re: Lienární algebra - Binární operace (2)
↑ Andrejka3:
takže osmiprvkovou množinou se myslí 4 rotace (90°, 180°, 270°, 360°) a 4 zrcadlení (2 jsou osy stran a dvě jsou úhlopříčky), přičemž bych si to vždy zapsal jako takovou jednoduchou permutaci a pak ty dvě permutace mezi sebou násobil, abych dostal tu výslednou, tak to mam sestrojenou tabulku. (jupí)
Komutativní zákon bych zjistil, zda je to podle diagonály symetrický (nebo prostě stejný).
no a asociativní zákon bych si asi vypsal, tedy: rotace 1 = a; rotace 2 = b; zrcadlení 2 = c
a tedy (a.b).c = a.(b.c)
pokud by platil Komutativní zákon, nemusil bych to vyšetřovat i do sloupců, akorát se mi zdá, že to je moc konkrétní... Je to přímo na příkladu, i když pro můj účel, by to nemuselo vadit...
Neutrální prvek existuje, to je 360°.
Inverzní prvek by existoval, pokud by se na každém řádku tabulky objevovaly všechny prvky právě jednou?
Souhlasí toto všechno? či jsem mimo? Dík
Offline
#11 04. 12. 2011 12:33
Re: Lienární algebra - Binární operace (2)
no a asociativní zákon bych si asi vypsal, tedy: rotace 1 = a; rotace 2 = b; zrcadlení 2 = c
a tedy (a.b).c = a.(b.c)
Tady se nemusíme namáhat. Tvrzení, že skládání zobrazení je asociativní operace je "známé". Pokud ho neznáš, měl by sis ho v budoucnu dokázat obecně (stačí trochu výrokové logiky).
Neutrální prvek existuje, to je 360°.
Ano, super.
mmnt musím odskočit, vrátím se brzy.
What does a drowning number theorist say?
'log log log log ...'
Offline
#13 04. 12. 2011 12:37
Re: Lienární algebra - Binární operace (2)
Tvrzení, že skládání zobrazení je asociativní operace je "známé"
To znamená, že by to platilo i u 6ti úhelníku? či 8,12,14? Podmínka je či není, že jsou pravidelné?
Offline
#15 04. 12. 2011 12:49
Re: Lienární algebra - Binární operace (2)
Vyšetři zvlášť komutativitu skládání mezi rotacemi.
Zamysli se nad inverzí rotace, třeba  .
.
Zamysli se nad inverzí zrcadlení.
Je skládání zrcadlení komutativní?
Je skládání uzavřeno na podmnožinu rotací?
Je skládání uzavřeno na podmnožinu zrcadlení?
Ty inverzní prvky jsou jednoduché. Pokud neděláš chyby ve skládání.
What does a drowning number theorist say?
'log log log log ...'
Offline
#16 04. 12. 2011 12:52
Re: Lienární algebra - Binární operace (2)
Aha, takže v pravidelném 8-mi úhelníku, pravidelném 13 úhelníku to taky bude platit? Nebo jen ve čtverci? V nepravidelných útvarech to nebude platit... To z toho chápu já... Správně?
Co jsou to přirozený dělitelé?
Offline
#17 04. 12. 2011 12:56
Re: Lienární algebra - Binární operace (2)
Aha, takže v pravidelném 8-mi úhelníku, pravidelném 13 úhelníku to taky bude platit? Nebo jen ve čtverci? V nepravidelných útvarech to nebude platit... To z toho chápu já... Správně?
Co přesně že nebude platit?
Přirozený dělitel celého čísla je jedna a to číslo samotné.
Mohl bys odpovědět na ty dílčí otázky... :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#18 04. 12. 2011 12:59
Re: Lienární algebra - Binární operace (2)
↑ Andrejka3:
inverzní k 90° je 270°
skládání zrcadlení není komutativní
Je skládání uzavřeno na podmnožinu rotací?
Je skládání uzavřeno na podmnožinu zrcadlení?
Tímto se myslí, jestli je nekonečno mnoho rotací? neni, takže to je uzavřený. ?
Stejně tak jestli, je nekonečně mnoho os, podle kterých se to dá zrcadlit? taky neni, takže je to uzavřený.
Offline
#19 04. 12. 2011 13:02
#20 04. 12. 2011 13:04
Re: Lienární algebra - Binární operace (2)
↑ lamnik:
Tím se myslí:
špatně jsem to formulovala, chtěla jsem napsat.
Je podmnožina rotací uzavřená na operaci skládání? Což znamená, když složíš dvě rotace, dostaneš rotaci?
Je podmnožina zrcadlení uzavřená na operaci skládání? Což znamená, když složíš dvě zrcadlení, dostaneš zrcadení?
Můžeš vyrobit vzoreček pro skládání rotací - ten je docela jednoduchý :)
What does a drowning number theorist say?
'log log log log ...'
Offline
#21 04. 12. 2011 13:18 — Editoval Andrejka3 (04. 12. 2011 13:28)
Re: Lienární algebra - Binární operace (2)
Ještě poznámka:
Mě by mohlo mást následující:
Když máme ten čtverec
_ _
_ _
tak ať tam jsou ta písmenka jakákoliv, tak třeba zrcadlení podle osy "uhlopříčka AC" 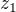 vypadá takhle
vypadá takhle
*
*
*
*
No a jestli ses ptal jestli existují podobné příklady, tak ano. Každý pravidelný n úhelník má symetrie, které tvoří podobnou algebru jako ta od čtverce. Extrémní případ je pak kružnice.
What does a drowning number theorist say?
'log log log log ...'
Offline
#22 04. 12. 2011 13:26
Re: Lienární algebra - Binární operace (2)
rotace a rotace dá vždy rotaci, to je uzavřená množina
ale to zrcadlení si nejsem jist, někdy mi vyjde že zrcadlení a zrcadlení mi dá rotaci...
to zrcadlení je možná jen podmnožina rotace?
vzorec pro rotaci... hmm

 ;
; ;
; ;
;
Tak teď se cejtim :)
Offline
#23 04. 12. 2011 13:29
Re: Lienární algebra - Binární operace (2)
tak ať tam jsou ta písmenka jakákoliv, tak třeba zrcadlení podle osy "uhlopříčka AC" vypadá takhle
*
*
*
*
tomuto nerozumím↑ Andrejka3:
Offline
#24 04. 12. 2011 13:37 — Editoval Andrejka3 (04. 12. 2011 13:43)
Re: Lienární algebra - Binární operace (2)
vzorec pro rotaci... hmm

Tak tak. Mohli bychom to upravit protože víme, že  na
na , kde "a mod (2pi)" je celociselny zbytek po deleni a/(2pi).
, kde "a mod (2pi)" je celociselny zbytek po deleni a/(2pi).
Ještě hezčí by to bylo, kdybychom prostě ty rotace označili: , jako identitu, rot. o devadesat,...
, jako identitu, rot. o devadesat,...
Pak totiz by vzorecek vypadal
A to je jednoduché to je takové kolečko 0,1,2,3 (čísla si dáš do kolečka a posouváš se po nich) :)
Hledej nejdřív inverzi zrcadlení 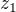 podle uhlopricky AC. (Preznacila jsem to z puvodni
podle uhlopricky AC. (Preznacila jsem to z puvodni 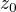 ).
).
EDIT: vsimla jsem si ze uz te napadnul izomorfismus algebry vsech rotaci ctverce s cyklickou grupou 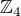
What does a drowning number theorist say?
'log log log log ...'
Offline
#25 04. 12. 2011 13:39
Re: Lienární algebra - Binární operace (2)
↑ lamnik:
Myslela jsem ten obrazek takhle: dejme tomu, ze chces provest slozeni: udelat rotaci o 90, pak udelat zrcadleni podle AC.
Postup: rotace o 90. No problem.
zrcadleni zrotovaneho. Podle jake osy mam zrcadlit? Podle nove osy AC (posunulo se to) nebo podle stare?
Odpoved: podle stare. V obrazku propoj ty hvezdicky a to jako mela byt primka ktera stoupa pod uhlem 45 stupnu, neboli stara uhlopricka AC v puvodnim ctverci
D C
A B
What does a drowning number theorist say?
'log log log log ...'
Offline


 a označit
a označit  .
. . Taková zobrazení se dají skládat. Můžeš si to představit takto: Složím operaci
. Taková zobrazení se dají skládat. Můžeš si to představit takto: Složím operaci  . Nejdřív čtverec otočím o devadesát stupňů a pak jej zrcadlím podle osy která je v té pozici, jak jsme si řekli. Dostaneš opět čtverec. Výsledná operace je opět operací symetrie, konkrétně nějaké zrcadlení (zkus si to)
. Nejdřív čtverec otočím o devadesát stupňů a pak jej zrcadlím podle osy která je v té pozici, jak jsme si řekli. Dostaneš opět čtverec. Výsledná operace je opět operací symetrie, konkrétně nějaké zrcadlení (zkus si to) . Máš zkoumat vlastnosti operace skládání symetrií.
. Máš zkoumat vlastnosti operace skládání symetrií. jsou množiny a
jsou množiny a  jsou zobrazení.
jsou zobrazení.