Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 12. 2011 11:29
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Hamiltonovsky graf
ahoj,som zo Slovenska a mam problem s jednim zadanim na Teoriu grafov.Uz som uplne zufala tak hladam nejakeho dobreho cloveka co by mi pomohol.
Zadanie znie: Určte, pre ktoré hodnoty a,b,c je graf 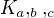 hamiltonovský.
hamiltonovský.
Prosim pomozte mi,mam z toho len klasifikovany zapocet a je za to 20 bodov...
Vopred vdaka.
Offline
#2 05. 12. 2011 11:40
#3 05. 12. 2011 11:49
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
Ja praveze neviem zistit co znamenaju tie indexy, 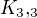 viem ako vyzera ale ked tam su 3 cisla...
viem ako vyzera ale ked tam su 3 cisla...
Offline
#4 05. 12. 2011 21:33
Re: Hamiltonovsky graf
↑ lucinka1991:Jedná se o tzv. kompletní tripartitní graf.
Popíšeme 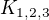 . Máme tři množiny vrcholů, 1-prvkovou, 2-prvkovou a 3-prvkovou.
. Máme tři množiny vrcholů, 1-prvkovou, 2-prvkovou a 3-prvkovou.
Dva vrcholy spojíme hranou právě tehdy, když patří do různých partit. Zkuste si graf nakreslit. Kolik bude mít hran? Mělo by jich v obrázku být 11.
Offline
#5 05. 12. 2011 23:34 — Editoval lucinka1991 (05. 12. 2011 23:37)
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
ano nakreslila som, a vyslo mi 11 hran.tento ale asi nie je hamiltonovsky ked nema stupen vrchola delitelny 2?A pri K1,1,3 mi vysiel pocet hran 7.
Offline
#6 05. 12. 2011 23:56
Re: Hamiltonovsky graf
↑ lucinka1991:Pozor, neplést eulerovské grafy a hamiltonovské grafy.
Graf 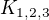 hamiltonovký je. Označím vrcholy v nejmenší partitě
hamiltonovký je. Označím vrcholy v nejmenší partitě 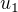 , v druhé partitě
, v druhé partitě 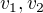 a v největší partitě
a v největší partitě 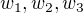 . Cyklus
. Cyklus 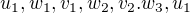 je hamiltonovský, protože obsahuje všechny vrcholy grafu.
je hamiltonovský, protože obsahuje všechny vrcholy grafu.
Offline
#7 06. 12. 2011 00:40
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar: aj K 1,1,3 je hamiltonovsky?pretoze sa mi to nejak nedari nakreslit,stale sa mi bud hrany pretnu alebo cez jeden vrchol prejdem 2x.
Offline
#8 07. 12. 2011 19:06
Re: Hamiltonovsky graf
↑ lucinka1991:Ne, graf 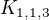 hamiltonovský není.V největší partitě jsou tři vrcholy. Mezi nimi není žádná hrana. Proto musíme z každého ze tří vrcholů jít do jiného vrcholu ve zbývajících partitách. To nejde.
hamiltonovský není.V největší partitě jsou tři vrcholy. Mezi nimi není žádná hrana. Proto musíme z každého ze tří vrcholů jít do jiného vrcholu ve zbývajících partitách. To nejde.
Offline
#9 07. 12. 2011 21:05
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar: mohla by tam platit podmienka 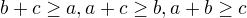 ??
??
Offline
#11 08. 12. 2011 13:36
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
cize to je vlastne riesenie tej ulohy?
Offline
#13 08. 12. 2011 20:35
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
hm tak to ma vobec nic nenapada, bude to mat nieco spolocne s hranami(ci je parny pocet alebo neparny?)?
Offline
#15 08. 12. 2011 21:51
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
no to mi je jasne,ale netusim teda ako tie intervaly vytvorit...
Offline
#16 09. 12. 2011 19:15
Re: Hamiltonovsky graf
Řekl jsem to neobratně. Množina přirozených čísel je "interval" celých čísel.
Zkrátka musíme vymezit, co za  dosadit můžeme a co ne. No a správná formulace je už v mém předchozím příspevku. Pokud v vyřešení stačí *říct* nikoliv *dokázat* nutnos a dostatečnosot nerovností
dosadit můžeme a co ne. No a správná formulace je už v mém předchozím příspevku. Pokud v vyřešení stačí *říct* nikoliv *dokázat* nutnos a dostatečnosot nerovností 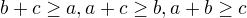 , tak je příklad vyřešen.
, tak je příklad vyřešen.
Offline
#17 09. 12. 2011 21:46
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
hm,tak v zadani pisu len ,ze Urcte pre ktore hodnoty,tak neviem. Ten dokaz je zlozity? Alebo cim by som mala zacat?
Offline
#18 10. 12. 2011 15:59
Re: Hamiltonovsky graf
↑ lucinka1991:Doporučuji začít tím, že si vyhledáte Diracovu a Oreho větu. Brali jste ji?
Offline
#19 10. 12. 2011 16:03
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
bohuzial nie,nasla som si ich na wikipedii,tam je aj nejaky dokaz ale vobec mu nerozumiem.
Offline
#21 10. 12. 2011 16:47
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar: nemame ziadnu literaturu k tomuto predmetu,on to je volitelny predmet kde mame za projekt 50 bodov,za tuto ulohu 20 a pisomnu pracu 30(na tu sme sa ucili z poznamok z cviceni).Mame len klasifikovany zapocet cize nikto sa tomu velmi nevenoval do hlbky,tak ani spoluziaci mi nevedia pomoct.
Offline
#23 12. 12. 2011 17:55
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
mame K1,2,3 ked na tento priklad aplikujeme Oreho vetu: dostanem pre moj priklad 2(b+c)>=a+b+c co je po uprave b+c>=a
cize plati Ka,b,c je hamilonovsky => b+c>=a
budem to dokazovat sporom cize znegujem vyrok: Ka,b,c je hamiltonovsky 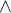 b+c<a
b+c<a
Ak vezmem ze  ma najvyssiu hodnotu a mozem ho spojit hranou iba s
ma najvyssiu hodnotu a mozem ho spojit hranou iba s 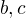 (kedze vrcholy rovnakej farby nemozu byt spojene) a sucet
(kedze vrcholy rovnakej farby nemozu byt spojene) a sucet 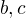 je mensi ako
je mensi ako  ,nakoniec sa dopracujem do bodu ked uz nebudem moct
,nakoniec sa dopracujem do bodu ked uz nebudem moct  spojit s
spojit s  alebo
alebo  a budem nutena ist do
a budem nutena ist do  => spor,nie je hamiltonovska kruznica pritomna cize plati prvy predpoklad
=> spor,nie je hamiltonovska kruznica pritomna cize plati prvy predpoklad 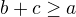
mohlo by to takto davat zmysel?
Offline
#24 12. 12. 2011 20:17
Re: Hamiltonovsky graf
lucinka1991 napsal(a):
↑ petrkovar:
mame K1,2,3 ked na tento priklad aplikujeme Oreho vetu: dostanem pre moj priklad 2(b+c)>=a+b+c co je po uprave b+c>=a
cize plati Ka,b,c je hamilonovsky => b+c>=a
Ne. Oreho věta udává dostatečnou, nikoliv nutnou podmínku pro existenci hamiltonovského cyklu.
Oreho větu bych použil pro zdůvodnění implikace: pokud  (
( je největší), tak víme. že
je největší), tak víme. že 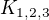 je hamiltonovský.
je hamiltonovský.
Naopak zbytek argumentace ukazuje, že pokud graf je hamiltonovský, musí být splněny nějaké nerovnosti.
Offline
#25 12. 12. 2011 20:27
- lucinka1991

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Hamiltonovsky graf
↑ petrkovar:
aj ten dokaz je zle?ja uz potom fakt neviem ako to ma byt...
Offline

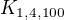 ?
?