Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 12. 2011 16:21
- FlyingMonkey

- Příspěvky: 758
- Reputace: 4
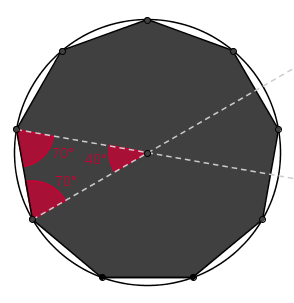
Tělesa - pravidelný devítiboký jehlan
Přeji hezký den,
Uploaded with ImageShack.us
s tímhle příkladem si nevím rady, neumím si přesně představit ten devítiboký jehlan.
Výšku bych pak asi spočítat dokázal - z pythagorovky, kde výška bude rovna součtu druhých mocnin "b" a uhlopříčky, která ale nevím kolik bude a i když jsem se snažil o nákres, nějak se mi to nedaří :)) Díky
Offline
#2 06. 12. 2011 16:35
Re: Tělesa - pravidelný devítiboký jehlan
Offline
#3 07. 12. 2011 09:11
- FlyingMonkey

- Příspěvky: 758
- Reputace: 4
Re: Tělesa - pravidelný devítiboký jehlan
Diky, ale nevychazi mi to, poradite prosim? (rychle prosim :D)
tg70 = v / a/2
spocitam si vysku v trojuhelniku rovnoramennem
dam do pythagorovku a spocitam si rameno x = 11 (z^2) + (a/2)^2
jenomze to kdyz prdnu do zaverecne pythagorovky nedava to smysl x^2 > b^2
pomuzete prosim? diky !
Offline
#5 07. 12. 2011 10:58 — Editoval ((:-)) (07. 12. 2011 12:46)
Re: Tělesa - pravidelný devítiboký jehlan
↑ L1ebeq:
Výška je približne 2,747... cm.
Prepona je približne 2,9 cm. Prečo by to bolo nelogické?
Dá sa zistiť aj cez sinus uhla alebo kosínus uhla a výšku trojuholníka ani netreba (má sa vyrátať výška telesa a známa je dĺžka bočnej hrany).
Offline