Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » binomicke a polynomicke koeficienty
#2 10. 12. 2011 16:39
Re: binomicke a polynomicke koeficienty
Navrhuji postupovat přímo: Vyberme si nějaký prvek  . Kolik je sudých podmnožin
. Kolik je sudých podmnožin  , které prvek
, které prvek  obsahují? A kolik le lichých podmnožin, které prvek
obsahují? A kolik le lichých podmnožin, které prvek  neobsahují.
neobsahují.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » binomicke a polynomicke koeficienty
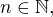


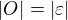 , ktorym sa ustanovuje bijekcia medzi
, ktorym sa ustanovuje bijekcia medzi 
