Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Lineární rekurentní rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 12. 2011 14:05
Lineární rekurentní rovnice
Přeji příjemnou sobotu všem. Snažím se vyřešit následující příklad.
Lineární rekurentní rovnice s konstantními koeficienty a kvazipolynomiální pravou stranou:
pro 
1) Vyřešte odpovídající homogenní rovnici. Obecné řešení napište ve tvaru neobsahujícím komplexní čísla.
2) Najděte partikulární řešení.
Svůj postup bohužel neuvedu, poněvadž zatím žádný není. Nějak moc netuším, jak začít. Už do toho od včerejška koukám a nevím, jak to uchopit. Na co konkrétního bych se ale zeptal: u prvního bodu (řešení homogenní rovnice) stačí když za pravou stranu dosadím místo kvazipolynomu nulu? Nebo je třeba to ještě na homogenní tvar nějak převést? Je tam psáno "... odpovídající homogenní...". Mohl by mi, prosím, někdo nastínit začátek nebo odkázat někam, kde je něco podobného vysvětleno?
BTW: Výsledek by byla dobrá věc, ale píšu z téhle látky test, postup je tedy cennější.
PS: Ještě bych jen doplnil. Toto zadání není z VŠB, nicméně když jsem naposledy řešil příklad z diskrétky, bylo mi doporučeno ho sem umístit. Omlouvám se tedy, pokud toto doporučení již neplatí :)
Předem děkuji.
Offline
- (téma jako vyřešené označil(a) Kondr)
#2 11. 12. 2011 18:53
Re: Lineární rekurentní rovnice
Tak jsem odhalil část postupu. Pomocí sofistikovaného softwáre (jenž nám byl doporučen :) ) jsem přišel na to, že charakteristický polynom této rovnice jest:
Reálné řešení:
Komplexní řešení:![kopírovat do textarea $x = -\sqrt[3]{-1}$](/mathtex/66/6696b92a54471484d7dd44871cfcc274.gif) a
a 
Což jsou vlastně kořeny. No a teď bych podle postupu z toho měl vydolovat obecné řešení přes bázi (nejspíš). Budu na tom nadále pracovat, pokud by někdo veděl, nestyďte se ozvat :D Konkrétně bych potřeboval - dle zadání - napsat to obecné řešení bez komplexních čísel.
Offline
#3 14. 12. 2011 22:30
Re: Lineární rekurentní rovnice
Ahoj ↑ mr.rubik:,
Tie korene sa daju "krajsie" vyjadrit
Mohol by si zacat riesit 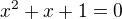
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 18. 12. 2011 18:18
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Lineární rekurentní rovnice
↑ vanok: Pro dořešení se nám hodí spíše tvar 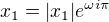 , k tomu má myslím kolega nakorčeno dobře (pak už se jen použije kuchařka).
, k tomu má myslím kolega nakorčeno dobře (pak už se jen použije kuchařka).
↑ mr.rubik: Bez komplexních čísel to --pokud vím -- nepůjde, ale ve skriptech určitě najdeš, že když jsou kořeny 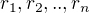 reálné (různé) a
reálné (různé) a 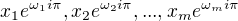 komplexní (různé) a
komplexní (různé) a 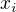 jsou jejich absolutní hodnoty, pak je obecné řešení tvaru
jsou jejich absolutní hodnoty, pak je obecné řešení tvaru 
(pokud jsou kořeny jednonásobné, jsou A, B, C konstanty, pro násobné kořeny jsou A,B polynomy proměnné k, C opět konstanty). Doufám, že toto je ten krok, který hledáš, tj. jak se zbavit komplexních čísel. Vyjádřit kořeny tvého polynomu v exponenciálním tvaru jistě zvládneš.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Lineární rekurentní rovnice (TOTO TÉMA JE VYŘEŠENÉ)