Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 23. 12. 2011 13:43
Re: Neurčitý integrál
↑ Deny77:
A proč považuješ za nutné počítat t dt ?
Standardním postupem by zde naopak bylo spočítat dx = x'(t) dt , kde x = x(t) je provedená substituce. Ve Tvém případě tedy x(t) vypočítáme z rovnice
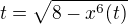 .
.
Pokud na této substituci trváš, pak je to samozřejmě Tvoje věc :-), kolega ↑ standyk: Ti chtěl nabídnout substituci šikovnější.
Offline
#6 23. 12. 2011 14:30 — Editoval Deny77 (23. 12. 2011 14:31)
Re: Neurčitý integrál
↑ Rumburak: Děkuju Vám hrozně moc za pomoc, na tý mojí substituci vůbec netrvám, jen mě napadla víš :) A ještě se prosím zeptám, co je před tím dx u tý substituce hned na začátku nahoře 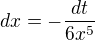 prosííím
prosííím
Offline

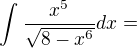 Vím zatím jen:
Vím zatím jen: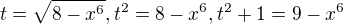 poradíte někdo jak mám vypadat to tdt?
poradíte někdo jak mám vypadat to tdt?
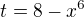
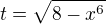 a
a 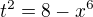 a
a 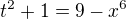

 a pak je jen vydělené tím
a pak je jen vydělené tím 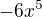 , takže
, takže