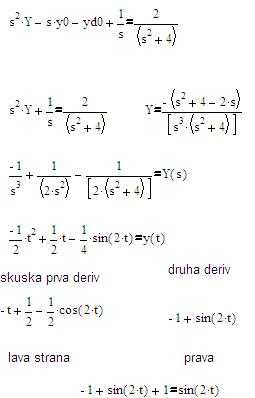Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 12. 2011 23:21
Laplaseova transformace
Dobrý den, vypočítal jsem si příklad, ale nevychází mi podle výsledku. Mohl by mi někdo říci kde je chyba?
zadani:
Pomocí L.T nalezněte řešení v intervalu [0,oo) dif. ronice y´´+1=sin2x,
podminky y(0)=0, y´(0)=0;
vyšlo mi Y(s)=2/((s^2)+4) + 1/((s^2)+1)
pak pres parcialni zlomky mi vyslo
a+c=0
a+d=0
a+4c=0
b+4d=2
dosadim...
Y(s)=2/((s^2)+(2^2))
po prevedeni brazu y(x)= sin(2x)
ve vysledku ma ale vyjit: y(x)=(x/2) -(sin2x/4)-(x^2/2)
Offline
#2 27. 12. 2011 23:35
Re: Laplaseova transformace
Asi máš špatně převedenou tu jedničku a pak jsi ji z nějakého důvodu dal do jmenovatele místo toho abys udělal společný jmenovatel. Takhle je zobrazená rovnice:


Dělal jsem to v rychlosti, tak snad jsem tam taky nehodil nějakou chybu :)
Offline
#4 28. 12. 2011 00:18
Re: Laplaseova transformace
dobrý den, tak jsem to znova prepocital....
vyslo mi ze ..
Y(s)=(2- s^2 -s)/(s^2+4) * 1/(s^2)
pres parciali zlomky mi vyslo
...
a+c=0
b+d=-1
4c=0
4d=-2
.. po dosazeni
¨...
Y(s)=-0,5/(s^2+4) -0,5/(s^2)
po prevedeni..
Y(x)=1/4*sin(2x)-1/2*t
opet mi to nevyslo podle vysledku...nevite co jsem udelal spatne ?
Offline