Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 09. 2008 23:21
Re: nerovnica
Vtip je v tom, že na levé straně jdou proměnné a, b, c libovolně zaměňovat, takže to musí jít i na pravé, tedy
Sečteme tyto 3 nerovnice a máme:
Dvojčleny na pravé straně zdola odhadneme AG nerovností jako
takže
Tato nerovnost se už snadno ukáže pomocí permutační ("mincové") nerovnosti, kde volíme obě množiny členů jako  .
.
Prosím kolegy o kontrolu, před několika minutami jsem se vrátil z koncertu a nevím jak moc mi to teď myslí…
Offline
#3 13. 09. 2008 23:34 — Editoval BrozekP (14. 09. 2008 00:11)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: nerovnica
↑ Olin:
Jsi si jistý tou první větou? Pokud by byla zadána třeba nerovnice  (která má řešení
(která má řešení  ), pak protože na levé straně můžeme zaměňovat, tak zaměněním na pravé straně dostaneme
), pak protože na levé straně můžeme zaměňovat, tak zaměněním na pravé straně dostaneme .
.
To ale třeba pro řešení původní rovnice a=1, b=-1 neplatí.
EDIT: Teď mi dochází, že to je spíš myšleno jako důkaz nerovnosti pro a,b,c>0 než řešení nerovnice s podmínkami a,b,c>0. Co jsi napsal nemůžeme použít v případě, že to budeme dokazovat tak, že vyřešíme nerovnici a všechny trojice a,b,c>0 budou řešením.
Myslím, že ty považuješ nerovnost za platnou, vyvodíš z ní něco dalšího co je zřejmě platné a pak prohlásíš nerovnost za splněnou. To buď není dobře, nebo jsem špatně pochopil tvůj postup.
Offline
#4 14. 09. 2008 01:07 — Editoval Marian (14. 09. 2008 22:04)
Re: nerovnica
↑ ktm22:
Nejprve vyřeším jednotlivě nezajímavé případy 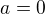 nebo
nebo 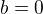 nebo
nebo 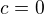 .
.
1. Je-li 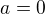 , vypadá daná nerovnost takto:
, vypadá daná nerovnost takto:
což je nerovnost mezi aritmetickým a geometrickým průměrem. Odtud platnost nerovnosti pro a=0 a libovolná nezáporná čísla b a c.
---------------------
2. Pro 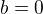 viz bod 1.
viz bod 1.
---------------------
3. Je-li 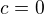 , provede se důkaz také elementárně - přenechávám zájemcům.
, provede se důkaz také elementárně - přenechávám zájemcům.
---------------------
4. Předpokládejme, že platí a>0, b>0, c>0. Pak existují kladná reálná čísla K,L taková, že b=K*a, c=L*a. Odtud nerovnost přejde na tvar
Taktéž je možné předpokládat, že existuje kladné číslo m takové, že L=m*K. Proto se dá nerovnost transformovat na tvar
Provedeme-li drobnou kosmetickou úpravu  , lze psát
, lze psát
Na levé straně je ale kvadratickým trinom (v proměnné M). K je parametr, K>0. Pro diskriminant levé strany platí
Ale výraz D(K) je pro všechna K>0 nekladný, což je snadno vidět. Proto nerovnost
platí pro studované proměnné a zároveň je ekvivalentní se zadanou nerovností. Tím je důkaz kompletní.
Offline
#5 14. 09. 2008 01:53
Re: nerovnica
↑ Olin:↑ BrozekP:
Souhlasím s BrozekP. Ta záměna nebude fungovat tak jednoduše.
No a mohl by ses ještě pochlubit, o jaký koncert se jednalo?
Offline
#6 20. 09. 2008 22:34
Re: nerovnica
Fajn, a co takhle to formulovat jako důkaz sporem? Jestliže neplatí původní nerovnost, tak jistě neplatí ani ty další dvě, které dostaneme záměnou. Součet všech těchto tří nerovností však platí, což je spor.
No, asi je to taky blbě.
Mimochodem, ten koncert bylo finále Janáčkovy klavírní soutěže.
Offline
#7 21. 09. 2008 10:42 — Editoval BrozekP (21. 09. 2008 10:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: nerovnica
↑ Olin:
"Dokážu" tvrzení, že všechna reálná čísla jsou rovna nule, tedy pro každé 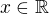 je
je  .
.
Pro  je rovnost zřejmá, uvažuji proto dále jen
je rovnost zřejmá, uvažuji proto dále jen 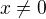 . Dokážu to tím "sporem" :-) Předpokládejme, že
. Dokážu to tím "sporem" :-) Předpokládejme, že  neplatí a tedy i
neplatí a tedy i  neplatí. Rovnice sečtu a získám tak
neplatí. Rovnice sečtu a získám tak 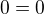 , což platí, je to tedy "spor". Platí tedy
, což platí, je to tedy "spor". Platí tedy  pro všechna reálná čísla x.
pro všechna reálná čísla x.
Při důkazu sporem vycházíme z tvrzení o kterých předpokládáme, že jsou pravdivá, a dojdeme k zřejmě neplatnému tvrzení (z pravdy tedy plyne nepravda, což není možné, takže náš předpoklad byl špatný). V tomto "důkazu" ale předpokládáme neplatnost jistého tvrzení a z tohoto neplatného tvrzení odvodíme jiné platné (z nepravdy plyne pravda, což je v pořádku, ale stále nevíme nic o tom, jestli náš předpoklad je správný - pravda také může plynout z pravdy).
Offline
#8 21. 09. 2008 12:23
Re: nerovnica
Eh, díky za vyvrácení mých nesmyslů. Mě se to od počátku celé nezdálo, ale líbilo se mi to.
Budu se dále snažit odpovídat jen při jasné mysli. Takhle to dopadá tragicky.
Offline
 .
.