Matematické Fórum

↑ O.o:

V matematice se často (například v definici limity, spojitosti funkce) řeckým písmenem označuje malé kladné číslo. Může být i velké, ale takové případy většinou nejsou zajímavé (pokud nás zajímají velká kladná čísla, obvykle je zase značíme nebo ).

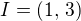Interval nemůže být roven intervalu , protože takové neexistuje. Např. pro dostaneme interval nebo pro 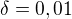interval .

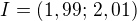V zadání neříkají jaké konkrétní máme, takže si jedno zvolíme. Na ose x tedy označíme dva body vzdálené o od čísla 2. Sestrojíme graf funkce h a na osu y vyneseme funkční hodnoty v krajních bodech intervalu I. Jak je z grafu zřejmé, funkce h zobrazuje množinu I na interval určený funkčními hodnotami v krajních bodech intervalu I.

↑ O.o: Nerekl bych, ze "se zapomnel zminit o malem delta". Pro takovy pripad preci neni vubec podstatne, jak velke delta je. Dokonce ani neni podstatne, jestli je delta kladne ci zaporne (kdyby bylo nulove, pak (2-delta,2+delta) je prazdna mnozina a neni co resit, resp. jako obraz zase vyjde prazdna mnozina, proc ne zapsana ve tvaru (5-2delta,5+2delta), ze). Pravdepodobne cela ta uloha miri nekde k pojmu okoli bodu, ale to je vedlejsi.

Pro reseni je podstatne, ze zadana funkce je spojita monotonni rostouci, z toho tedy plyne, ze chceme-li zjistit, na jaky interval J se zobrazi nejaky jiny interval I, staci dosadit krajni body intervalu I. Dale diky tomu, ze jde o primku, tak "stred" intervalu I se zobrazi na stred intervalu J, tedy interval J muzeme snadno zapsat ve tvaru "stred plus minus neco", mame-li interval I nachystan ve tvaru "stred plus minus neco". To pro obecnou monotonni rostouci funkci samozrejme neplati.

Poznamka: Byla-li by funkce sice spojita monotonni, ale klesajici, plati to o zobrazovani intervalu na interval podobne, akorat pravy krajni bod intervalu I se zobrazuje na levy kraji bod intervalu J a opacne.

↑ O.o: Interval znamena, ze stred intervalu je v bode a cely interval "je dlouhy" , tedy jako bych si predstavil vse mezi o doprava a o doleva od dvojky. Mohl bych tedy rict neco jako ze polomer toho intervalu je .

Zadana funkce zobrazi stred intervalu I, tedy dvojku, na 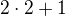, tedy na petku. Co se stane s polomerem zobrazovaneho intervalu? No na co se zobrazi jeden z krajnich bodu intervalu I, treba bod ? Preci na . Tedy polomer intervalu J bude . Proto tedy vysledek . Tady jsem vyuzil toho, ze vim, ze zkoumanou funkci je primka.

Obecneji bych (pri tvem znaceni ) to mel delat takto:
, , tedy interval se zobrazuje na interval .

↑ O.o: Uvedl jsem vlastne dve reseni. Jedno textove delsi, i kdyz vlastne jednodussi (to prvni - zvlast vypovet stredu a polomeru intervalu J) a druhe takove "otrocke", kdyz zobrazis oba krajni body intervalu I (posledni veta prispevku).

Abych teda vysvetlil to, na co se ptas. Je nam jasne, ze zobrazujeme interval I se stredem ve dvojce a polomerem delta. Diky tomu, ze jako funkci h(x) mame rostouci primku, je nam take jasne, ze obrazem intervalu I bude interval J se stredem v h(2)=5 a polomerem zatim neznamym. Je nam take jasne, ze krajni body intervalu I se zobrazi na krajni body intervalu J a vsechno bude spojite.

Zajimam-li se o polomer intervalu J, staci mi tedy zobrazit nektery z meznich bodu intervalu I pomoci primky h a od vysledku odecist stred intervalu J, ktery uz znam, tedy h(2)=5. Odtud onen vysledek, ze polomer intervalu J bude h(2+delta)-h(2)=2*delta.

Uz je to jasne?

Poznamka 1: Vsechny vypocty v tomto vlakne se toci kolem toho, ze h(x) je primka. Kdyby to tak nebylo, ale slo stale o spojitou rostouci monotonni funkci, treba h'(x)=x^2 pro nezaporna x, tak obrazem intervalu I=(2-delta,2+delta) by byl interval J=(4-4*delta+delta^2, 4+4*delta+delta^2). Porad by totiz stacilo zobrazit krajni body intervalu I a vysledny interval J by lezel mezi jejich obrazy ve funkci h'. Zapsat interval J ve tvaru "stred plus minus neco" by nebylo tak snadne: stred 4+delta^2, polomer 4*delta. Zajmena pro nelinearni funkci nemusi platit, ze stred intervalu I se zobrazuje na stred intervalu J.

Poznamka 2: Pro primku plati, ze ma-li interval I polomer rI, pak interval J ma polomer rJ (v nasem pripade bude J vzdy dvakrat vetsi nez I), at je I umisten kdekoli na x-ove ose. To samozrejme obecne neplati. Jako priklad se da pouzit treba zrovna priklad z Poznamky 1. Kdyby I=(1-delta,1+delta), tak J=(1-2*delta+delta^2, 1+2*delta+delta^2), tedy polomerem J by bylo 2*delta, zatimco v Poznamce 1 vyslo 4*delta, pricemz polomer intervalu I byl v obou pripadech stejny, a to delta.