Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dľžka zlatej špirály (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 01. 2012 09:12
dľžka zlatej špirály
žiadam pomoc: rovnica pre dlžku zlatej špirály.
rovnica zlatej špirály: r=1*exp(0,00267*alfa), alfa je v stupňoch
rovnica vznikla z podmienok:
alfa=0, r=1, a=1
alfa=90, r=sqrt(fi), b=0,00267
fi=(1+sqrt(5))/2
Offline
- (téma jako vyřešené označil(a) jelena)
#2 10. 01. 2012 12:03
Re: dľžka zlatej špirály
Ni moc, ni bohatství, jen vědění žezla trvají!
Offline
#3 10. 01. 2012 12:19
Re: dľžka zlatej špirály
Ni moc, ni bohatství, jen vědění žezla trvají!
Offline
#5 11. 01. 2012 00:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: dľžka zlatej špirály
↑ Zoli7114:
Zdravím,
mohli jste počítat podle vzorce pro délku křivky v polárních souřadnicích. Nebo podle kterého vzorce jsi počítal?
Těžko někdo bude kontrolovat číselné výpočty, spíš postup. Děkuji.
Offline
#6 11. 01. 2012 01:02
Re: dľžka zlatej špirály
↑ jelena:
Zdravím. použil som vzorec z nemeckej wikipedie :
http://de.wikipedia.org/wiki/Spirale
konrétne: 
ďakujem.
Offline
#7 11. 01. 2012 09:40 — Editoval Honzc (13. 01. 2012 14:14)
Re: dľžka zlatej špirály
↑ Zoli7114:
Tak tedy:
Nejdříve je třeba ze zadání určit rovnici zlaté spirály. ( budeme brát v radiánech)
budeme brát v radiánech)
Platí:
Pro naše zadání: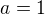
 kde
kde 
a tedy rovnice zlaté spirály v polárních souřadnicích ( ) je:
) je:
Pro délku křivky platí:
pro náš příklad:


![kopírovat do textarea $l=\sqrt{1+b^{2}}\int_{0}^{\frac{\pi }{2}}e^{b\alpha}d\alpha =\frac{\sqrt{1+b^{2}}}{b}[e^{b\alpha}]^{\frac{\pi }{2}}_{0}=$](/mathtex/92/92b983349bdcf43bbb4845f6671c8f20.gif)

Po editaci
Příklad je spočítán pro čtvrtinu závitu, tj pro 
Celý závit ( ) by měl délku
) by měl délku 
Po druhé editaci:
Co je ovšem ještě zajímavější je toto:






Ještě malá tabulka:
kde je vždy délka úseku (od-mez v řádku do-mez ve sloupci) dělená konstantou 
A nakonec toto:
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » dľžka zlatej špirály (TOTO TÉMA JE VYŘEŠENÉ)

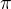 )=10,686
)=10,686
