Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 01. 2012 20:54
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Kartézský součin jako grupa - značení
Ahoj,
začnu obecně a pokud by byl text nejasný, doplním detaily (které však nyní mohou být zbytečné). Tedy - mějme grupu G s generátorm g, grupu H s generátoem H. Uvažujme grupu K:=GxH (podobnou kontrukci můžeme vidět u tvz. přímého nebo polopřímého součinu grup), jejíž prvky jsou tedy uspořádané dvojice (gi;hj), gi z G, hj z H a kde grupová operace je definována "po složkách".
V textu, který se této problématiky týká, jsem však našel výrazy určující prvek z K, které jsou např. tvaru g*h, g*h*h, apod. Ovšem členy tohoto výrazu nejsou uspořádané dvojice (jak by dle definice k měly být), což mě trošku mate. Rád bych se zeptal, zda není v podobných případech zvykem ztotožňovat např. (g;1) a g, resp. (1,h) a h - potom by např. první výraz g*h byl tvaru (g;1)*(1;h) - a pak by bylo vše jasné.
Díky za odpovědi, případně zodpovím dojasňující otázky.
"Máte úhel beta." "No to nemám."
Offline
#2 04. 02. 2012 13:02 — Editoval vanok (04. 02. 2012 13:03)
Re: Kartézský součin jako grupa - značení
Ahoj ↑ check_drummer:,
Toto je ozaj zaujimava otazka.
Pises toto:
mějme grupu G s generátorm g, grupu H s generátoem H. Uvažujme grupu K:=GxH (podobnou kontrukci můžeme vidět u tvz. přímého nebo polopřímého součinu grup), jejíž prvky jsou tedy uspořádané dvojice (gi;hj), gi z G, hj z H a kde grupová operace je definována "po složkách".
Co sa tyka priameho sucinu mame dokonca viac:
Pre kazde 2 grupy  ; ich priamy sucin
; ich priamy sucin 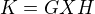 je jednoducho kartesiansky sucin
je jednoducho kartesiansky sucin  a
a  , zo zakonom
, zo zakonom 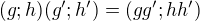
 a
a  su potom respektivne isomorfne z
su potom respektivne isomorfne z a
a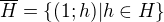 .
.
Naviac je jednoduche vidiet ze  ako aj
ako aj 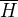 su normalne v
su normalne v 
a ze a
a
Priklad:
Ak p, q su nesudelitelne mame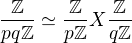
Pozor to neplati ak p, q nie su nesudelitelne.
Mame napriklad  nie je isomorfna z
nie je isomorfna z 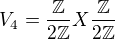
Ak mas na toto otazky, napis.
A o polo-priamom (semi-direct) sucine napisem neskor, lebo to je dost dlhe.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 05. 02. 2012 19:14
Re: Kartézský součin jako grupa - značení
↑ check_drummer:
Co sa tyka "semidirect product"
tu je celkom dobre vysvetlenie:
http://en.wikipedia.org/wiki/Semidirect_product
Ale cim skor to tu doplnim, aby to bolo este jasnejsie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 07. 02. 2012 20:34 — Editoval vanok (07. 02. 2012 20:56)
Re: Kartézský součin jako grupa - značení
Pouzijem tie iste notacie ako v prispevku Wikipedia...co umozni lahsie sledovat tento dokument.
Uvedomme si najprv, ze nas problem je :
Bud  grupa,
grupa,  normalna podgrupa grupy
normalna podgrupa grupy  a
a  faktorová grupa
faktorová grupa  podle normalnej podgrupy
podle normalnej podgrupy 
Co hladame je zo znalosti  a
a  zrekonstituvat grupu
zrekonstituvat grupu  .
.
Vsebecny problem je ak su zname dve grupy  a
a  najst vsetky grupy
najst vsetky grupy  , take aby toto schema bolo exaktne:
, take aby toto schema bolo exaktne:
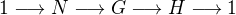
Vtedy sa hovori ze taka  je EXTENTION
je EXTENTION  na
na  ( ale niekde sa to vola aj
( ale niekde sa to vola aj  na
na  )
)
Tento vseobecny problem je komplikovany...( cf. kniha Hall:Theory of groups$)
Tu ako naznacil kolega ↑ check_drummer: si pozrieme na dva specialne jednoduche pripady:
priamy sucin grup, a polopriamy sucin grup.
Priamy sucin sme uz dost popisali.
Na polopriamy sucin, tu dame navyse, ako vo Wikipedii, nejake pozmamky, co pomozu lepsie pochopit tento pojem.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 08. 02. 2012 14:00 — Editoval vanok (08. 02. 2012 14:01)
Re: Kartézský součin jako grupa - značení
Ked citam anglicku verziu, tak sa mi to zda velmi dobre vysvetlene ( tak pridam len niekolko malo komentarov, co mozu byt uzitocne)
Semidirect products and group homomorphisms
Let G be a semidirect product of the normal subgroup N and the subgroup H.
Let Aut(N) denote the group of all automorphisms of N.
The map φ : H → Aut(N) defined by φ(h) = φh, where  for all h in H and n in N, is a group homomorphism.
for all h in H and n in N, is a group homomorphism.
Together N, H and φ determine G up to isomorphism, as we show now.
Given any two groups N and H (not necessarily subgroups of a given group) and a group homomorphism φ : H → Aut(N), there is a new group 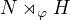 (or simply
(or simply 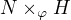 ), called the semidirect product of N and H with respect to φ, defined as follows.
), called the semidirect product of N and H with respect to φ, defined as follows.
As a set,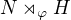 is the cartesian product
is the cartesian product  .
.
Multiplication of elements in 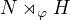 is determined by the homomorphism φ. The operation is
is determined by the homomorphism φ. The operation is
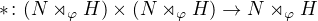
defined by
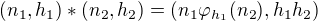
for n1, n2 in N and h1, h2 in H.
This defines a group in which
the identity element is 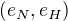
and the inverse of the element (n, h) is  .
.
Pairs 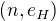 form a normal subgroup isomorphic to N, while pairs
form a normal subgroup isomorphic to N, while pairs  form a subgroup isomorphic to H.
form a subgroup isomorphic to H.
Presnejsie 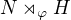 ma dve podgrupy
ma dve podgrupy je isomorfne z
je isomorfne z  (ktora je normalna v
(ktora je normalna v 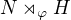
a 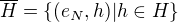 je isomorfne z
je isomorfne z  ( vseobecne nie je normalna v
( vseobecne nie je normalna v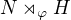 )
)
The full group is a semidirect product of those two subgroups in the sense given above.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 11. 02. 2012 17:12 — Editoval vanok (11. 02. 2012 20:41)
Re: Kartézský součin jako grupa - značení
Ani v tejto casti netreba nic pridavat
Conversely, suppose that we are given a group G with a normal subgroup N and a subgroup H, such that every element g of G may be written uniquely in the form g=nh where n lies in N and h lies in H.
Let φ: H → Aut(N) be the homomorphism given by 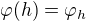 , where
, where

for all n in N and h in H. Then G is isomorphic to the semidirect product 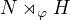 ; the isomorphism sends the product nh to the tuple (n,h).
; the isomorphism sends the product nh to the tuple (n,h).
In G, we have the multiplication rule
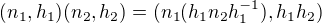 .
.
A version of the splitting lemma for groups states that a group G is isomorphic to a semidirect product of the two groups N and H if and only if there exists a short exact sequence

and a group homomorphism γ : H → G such that 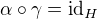 , the identity map on H. In this case,
, the identity map on H. In this case,
φ : H → Aut(N) is given by 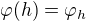 , where
, where
 .
.
If φ is the trivial homomorphism, sending every element of H to the identity automorphism of N, then  is the direct product
is the direct product 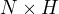 .
.
Poznamky:
A) je aj tu bijektivne z
je aj tu bijektivne z  ako mnozinovy sucin
ako mnozinovy sucin
B) "nasobenie" nie je to iste ako v pripade priameho sucinu. tu je
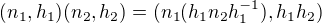
C) operacia z  na
na  , nie je len mnozinova,
, nie je len mnozinova,  operuje automorfizmany grup na
operuje automorfizmany grup na 
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 11. 04. 2012 12:30 — Editoval Andrejka3 (11. 04. 2012 12:31)
Re: Kartézský součin jako grupa - značení
Ahoj, děkuji kolegovi ↑ vanok:.
Prošla jsem si to a rozumím tomu po tuto část:
...
...
Tady už nerozumím symbolice. Lze nějak vágněji říct, co toto tvrzení znamená / jaké jsou jeho důsledky?
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 11. 04. 2012 12:58
Re: Kartézský součin jako grupa - značení
ahoj,
teraz mam malo casu,
tak posielam len tuto adresu kde sa pise o "exact sequence"
Pojem, co treba dobre asimilovat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
