Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 10. 2008 22:08
slovni ulohy
ahoj,mam takovou ulohu a ted uz mi to nejak nemysli,byl bych hrozne vdecnej za pomoc jak to vypocitat!
Pan x vybudoval ovocny sad.Třetinu vsech stromu v sade tvorili jablone,25% hrusne a zbyvajicich 250 stromu byly peckoviny.Urcete kolik jabloni a kolik hrusni mel pan x v sadu?
Offline
#4 09. 10. 2008 16:06
Re: slovni ulohy
ahojky ..... mám jeden takový ukol ..... mám vypočítat příklad :
Jedna část střechy má tvar rovnoramenného lichoběžníku, jehož tri strany pokryté
hřebenáči jsou stejně dlouhé. Dolní strana s okapovým žlabem je o 9 metru kratší, než
je součet délek tří zbývajících stran. Obvod této lichoběžníkové strany střechy se
rovná 27 m. Kolik tašek je třeba na její pokrytí, jestliže na 1m čtvereční se jich spotřebuje 16
a ztráty úpravou tašek štípáním a odsekáváním činí 8 %.
Moc vás prosím pomožte mi s tím ...... už dlouho si s tím lámu hlavu ale nějak pořád nevím jak na to byla bych vám moc vděčna ...... děuji předem
Offline
#6 09. 10. 2008 16:51 — Editoval O.o (09. 10. 2008 16:56)
Re: slovni ulohy
↑ M-a:
Máš někde výsledky, nejsem an tyhle úlohy zrovna nejkvalitnější .)?
1) Takže bych začal obrázkem rovnoramenného lichoběžníku:
a
____
a / \ a
---------
b
2) kde platí, že:
a) Součet tří stran je roven délce čtvrté strany, která má rozdílnou délko od původních, bez devíti metrů
(a+a+a = b-9)
3a = b-9
b) a obvod lichoběžníku je roven dvacetisedmi, tj:
3a+b = 27
3) Zjistit strany znamená vyřešit soustavu rovnic (viz. výše):
3a = b-9
3a+b = 27
=> a = 3 => b = 18
4) Obsah lichoběžníku se snad počítá jako:
a+b
S = ------- * v
2
(Doufám ,že jsem se nepřestřelil)
5) Do obrázku tedy zakreslíme v, abychom mohli pokračovat.
a
L___________
/| \
a / | v \ a
/_|_____________\
P Q b
Z toho když známe a a b dokážeme zjistit v. Trojúhelník PQL totiž má pravýúhel a to u bodu Q (úhel PQL).
Trojúhelník PQL: b-a
|PQ| = ------ = 5
2
|PL| = a = 3
|QL| = v = ?
pythagorova věta: (|PQ|)^(2) + (|LQ|)^(2) = (|PL|)^(2) dosadíme a zjistíme, že |QL| = v = (odmocnina z 6)
6) Výpočet obsahu:
Dosdíš si do vzorečku (když vše znáš) a výsledek je (hodně zaokrouhleně): S = 25,72 m^(2)
7) Trojčlenka na pokrytí střechy beze ztrát:
| 1 m^(2) ................ 16 tašek |
v 25,72 m^(2) ................ x tašek v
-----------------------------------------------
x = 16 * 25,72 = 411,52 (znovu jsem hodně zaokrouhlil)
Těchto 411,52 metrů je potřeba na pokrytí bez ničení tašek, takže je to vlastně 100-8% = 92%
8) Trojčlenka na procenta ztrát:
| 411,52 tašek ................ 92% |
v x tašek ................ 100% v
--------------------------------------------
x = 447,30 tašek
EDIT:
Jednotky jsou většinou metry nebo metry čtvereční, nebaví mne to stále psát.
Je docela možné, že jsem to někde zeslonil a to pořádně, nemám u sebe tužku ani papír, tak je to trochu sázka do loterie, obzvláš? převádění ze zadání .)
EDIT II:
Koukám, že Chrpa má jiný výsledek, tak má ltoerie nevyšla, nechávám to tu, aby všichni viděli, jaká jsem trubka .(
PS: Co jsou to ty hřebenáče prosím?
Offline
#8 09. 10. 2008 17:26 — Editoval Chrpa (09. 10. 2008 17:29)
Re: slovni ulohy
↑ O.o:
Ramena a kratší stranu lichoběžníku označme jako x
Delší stranu lichoběžníka jako y
y = 3x - 9
Obvod lichoběžníku je 27 m tj:
3x + 3x - 9 = 27 (jestli dobře čtu)
6x = 36
x = 6
y = 3x - 9 = 18 - 9 = 9
Plocha střechy licoběžníku je: (x+y)*v/2 v je výška musí platit: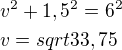 1,5 = (9-6)/2
1,5 = (9-6)/2
A teď je otázka zda ta střecha má i druhou stranu. Já když to počítal tak jsem myslel, že ty střechy jsou vlastně dvě.
Pokud ne pak obsah střechy bude:
Na 1m^2 potřebujeme 16 tašek tj. celková potřeba tašek bude: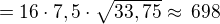
Kdybychom žádnou nerozbili, pak by jich bylo potřeba 698 my jich však potřebujeme o 8 % víc tj:
Pokud by to mělo i druhou stranu pak by to bylo 2 krát víc tašek
Offline
#10 09. 10. 2008 17:33 — Editoval Chrpa (09. 10. 2008 17:38)
Re: slovni ulohy
↑ O.o:
Ano napsal protože rozměry střechy jsou 9 a 3*6 metrů
Dohadovat se můžeme zda je to klasická střecha tj. zda má jednu i druhou stranu nebo má jen jednu stranu.
Já si to představuji tak, že by ta střecha třeba nad kůlnou byla přilepena k nějaké zdi. (teda ta kůlna)
Hřebenáče jsou vlastně "tvarovky", které kryjí hřeben střechy, aby do ní nezatékalo. I z toho bych usuzoval, že předmětná střecha má dvě plochy.
Offline
#12 10. 10. 2008 19:16
Re: slovni ulohy
tak už vím správný výsledek ...... :-) (chrpa to měl dobře)
když jsem to vypočítala vyšlo mi 751,5 tašky po zaokrouhlení 752 a kdyby to bylo jako kdyby na ty 2 střechy tak to vyšlo 1504 ...... Moc vám děkuji za ochotu ( akorád jsem to vypočítala trochu jednoduššeji než vy .... ale výsledek souhlasí )
Offline
#13 27. 10. 2008 09:49
Re: slovni ulohy
potřeboval bych vypočítat a vysvětlit tento příklad: Dvě písařky napsaly dohromady 65 stránek strojopisu. I když první z nich psala o hodinu déle než druhá, napsala o 5 stránek méně, nebo? druhá písařka píše za hodinu o 2 stránky více než první. Kolik stránek za hodinu napíšou obě dohromady? my jsme ve škole počítali podobné příklady se vzorcem: rychlost * čas = dráha (přitom na místo dráhy jsme vždy dosadili číslo 1) Nevím jak to do tohoto vzorce dosadit.
Offline
#17 27. 10. 2008 10:44
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑ martas277:
Jen ti napovím toto:
První písařka napsala za x hodin o 5 stránek méně než druhá písařka za (x-1) hodin
Znamená to, že první písařka napsala za x hodin 30 stránek a druhá písařka napsala za (x-1) hodin 35 stránek.
Nikdo není dokonalý
Offline
#19 27. 10. 2008 11:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: slovni ulohy
↑ ttopi:
Písařky jedou :-) (zajimavé je, že první dojem je tuto úlohu zařadit do "společné práce" a ono to je úloha na pohyb)
http://forum.matweb.cz/viewtopic.php?id=55&p=5
http://forum.matweb.cz/viewtopic.php?id=55&p=2 - příspěvek 39
Hezkou zábavu :-)
Offline
#20 27. 10. 2008 11:36
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑ jelena:
Já věděl, že se to tady už řešilo. Ale protože nerad prozkoumávám fórum tak jsem si to spočítal ještě jednou
a překvapivě mě vyšlo to samé jako Jeleně v příspěvku 39.
Toto je zcela jasně příklad na společnou práci. Nevím proč do toho v té škole míchají příklady na pohyb.
Nikdo není dokonalý
Offline
#21 27. 10. 2008 11:50 — Editoval ttopi (27. 10. 2008 11:55)
Re: slovni ulohy
Matematika je rozmanitá věda, tady to vidíte :-)
Když se tam ale podívám na ty zlomky, co jste tam psali, tak to není nic jiného než podíl práce/výkon což je shodné s práce/rychlost, obojí pak vychází v čase t :-)
oo^0 = 1
Offline
#22 27. 10. 2008 12:03
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: slovni ulohy
↑ ttopi:
Zdravíčko
Ale pak v tom mají ti žáci neuvěřitelný zmatek a místo toho, aby to bylo jasné jim to ještě víc zamotají.
Pak už opravdu neví, která bije.
Nikdo není dokonalý
Offline
#23 28. 10. 2008 18:26
Re: slovni ulohy
Chtěl jsem se prosím zeptat na tuto slovmí úlohu: K naplňování i vyprazdňování palivové nádrže o objemu 2400 m^3 slouží stejné čerpadlo. Při vyprazdňování je jeho výkonnost o 10 m^3 za minutu vyšší než při naplňování. Proto vyprázdnění nádrže trvá o 8 minut méně než její naplnění. Určete, kolik m^3 nádrže naplní čerpadlo za 1 minutu.
Offline
#25 28. 10. 2008 19:06 — Editoval Chrpa (28. 10. 2008 19:12)
Re: slovni ulohy
↑ martas277:
Označme: x - výkon čerpadla při napouštění (m^3/min) máme určit
p - počet minut potřebných k napuštění 2400 m^3
Platí: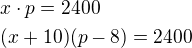

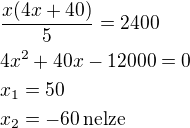
Výkon čerpadla je při napouštění 
Zkouška:
Při uvedeném výkonu se nádrž naplní za 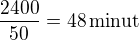
Při výkonu o 10m^3/min vyšším při vypouštění se nádrž vyprázdní za: 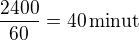
Rozdíl časů mezi vypouštěním a napouštěním je 8 minut což je v souladu se zadáním úlohy.
Offline